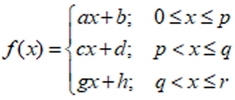We have already encountered piecewise-defined functions, which are functions that use different equations over different "pieces" of their domains. We have also already encountered linear function models. Now, it's time to meld these two concepts together. Let's take a look at what we need to know about using piecewise functions to model mathematical situations.
When setting up a linear piecewise-defined model, the main focus will be on the domain. Where will the "pieces" of the domain start and stop? Which equations correspond to which sections of the domain?
Focus on the domain!
Establish where the "pieces" start and stop.
Using y = mx + b, along with plotting points,
will be valuable methods for graphing sections of piecewise functions. |

|
|
Keep in mind that here are three styles of piecewise functions that are of interest to us.
1. basic piecewise functions 2. absolute value piecewise functions
3. step piecewise functions
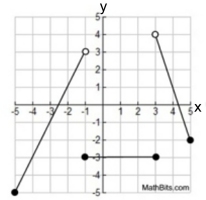
Basic Piecewise Function |
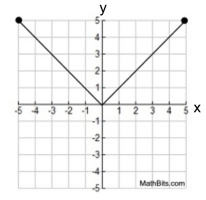
Absolute Value Piecewise Function |
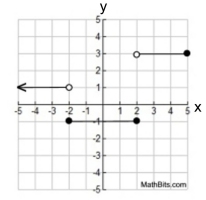
Step Piecewise Function |
The graphs above show only one possibility of each type of graph.
There are countless numbers of graphs that can be formed using line segments, points, and rays.
These graphs illustrate the "types" of functions you will see when modeling piecewise functions.
Remember that a linear piecewise function will come in a general form such as:
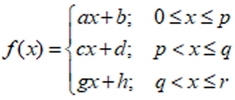

| Let's take a look at some things you should remember when piecewise "modeling": |
Regarding modeling linear functions, we saw a list of five things we need to remember.
This list will still apply to modeling piecewise linear functions:
1. identify your variables unless already specified.
2. label your answers where appropriate
3. state the domain of the function indicating any limitations
4. properly prepare graphs
5. read carefully to secure all details
|

Now, let's add a few more items to the list that are specific to piecewise functions:
Be careful how you deal with the endpoints of segments or rays.
If the domain tells you to include ( < , > ) that endpoint, use a closed circle.
If the domain tells you NOT to include ( < , > ) that endpoint, use an open circle.
6. Deal with endpoints.
closed circle = include the point; open circle = don't include the point |
 NEVER have two closed endpoints directly over one another. NEVER have two closed endpoints directly over one another.
If this happens, you no longer have a function.

Don't be surprised if your piecewise graph model has "holes" or "breaks".
Piecewise models can be either discontinuous functions, or continuous functions.
If you can draw the entire graph without removing your pencil from the paper,
your graph is continuous. If not, your graph is discontinuous.
| 7. Piecewise graphs may be continous or discontinuous. |

Piecewise model graphs may be both increacsing and decreasing across their domains.
Because a piecewise graph deals with more than one function,
the piecewise graph may be both rising and falling across its domain.
8. Piecewise graphs may be both increasing and decreasing across their domains. |

Because piecewise functions deal with several equations,
they also deal with several restricted domains.
You need to determine where each "piece" of the function
will start and stop on the graph.
9. Focus on the domain.
Determine where the "pieces" start and stop. |

When you are working with word problems, you must always ask yourself,
"Do my results (my graph) make sense?"
Or did I just try to sell "half a book?", or "extend a roof line into infinity?"
Should my graph be a solid line, or a series of dots?
10. Be sure your results are realistic!
Don't end up selling half of a book.
|

Check out Piecewise Modeling problems.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|