|
Another function that falls under the category of a piecewise-defined function is the Step Function.
The step function is made up of a series of different constant values on given horizontal intervals. Each "piece" is actually a constant function.
The graph looks like a series of "steps" since it consists of a series of horizontal segments with jumps in between, and as such, is often called
the "staircase function". |
 |
 |
A step function is a piecewise-defined function in which every piece is a horizontal line segment (or a point or horizontal ray).
(Also called a staircase function, or a piecewise constant function.) |
|
If you are tempted to connect the dots in a step function to draw the staircase, don't!
There are no vertical segments in a step function. There are no vertical segments in any function.

 A Step Function is a Piecewise-defined Function: A Step Function is a Piecewise-defined Function: |

Graph the function defined as:
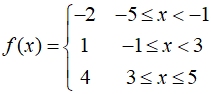
Notice all of the "constant" values as the equations.
We know that these constant values will produce horizontal linear segments on their restricted domains.
So, just start placing the segments.
Be sure the segment endpoints coincide with the restricted domains regarding open or closed circles.
Note the "step", or "staircase" appearance. |
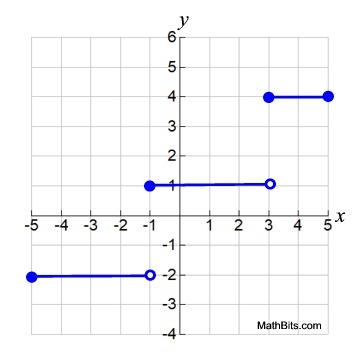 Domain of entire function: [-5,5] or -5 < x < 5 Domain of entire function: [-5,5] or -5 < x < 5
Range of entire function: {-2, 1, 4}
only 3 values
|
 Notice: When working with step functions, the "bars" (line segments) do not have to be of the same length nor have the same vertical distance between them Notice: When working with step functions, the "bars" (line segments) do not have to be of the same length nor have the same vertical distance between them


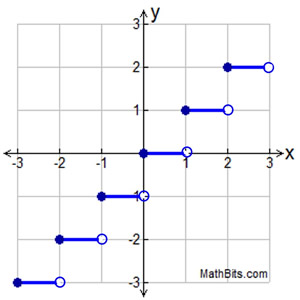
Graph the function defined as:
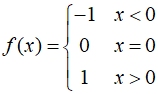
In this step functions, we see the appearance of a single point as a "piece" and two rays as "pieces".
This function does not have the "staircase look" that some of the step function possess, but it does meet the definition of a step function.
|
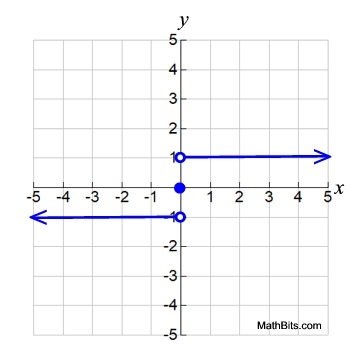 Domain of entire function: All Real Numbers Domain of entire function: All Real Numbers
Range of entire function: {-1, 0, 1}
only 3 values
|


Graph the function defined as:
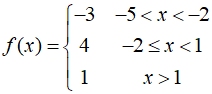
In this step functions, we have a combination of line segments and a ray as the "pieces".
In this graph, the "steps" do not all progress upward from left to right. This is an "up and down stair" effect.
Notice the problem at x = 1. Since both endpoints are open circles, there is NO plotted value at x = 1. This opening must be noted in the statement about the domain of the entire function:
all Reals greater than -5 but not {1}.
|
 Domain of entire function: Domain of entire function:
All Real Numbers > -5 but not {1}
Range of entire function: {-3, 1, 4}
only 3 values
|


Several step functions are referred to by a specific name.
One of the more common "named" step functions is the Greatest Integer Function. The Greatest Integer Function's rule is that the y-coordinate is the "greatest integer less than or equal to the corresponding x-coordinate".
If the x-coordinate is an integer, the y-coordinate is that same integer value.
If the x-coordinate is not an integer, the y-coordinate is the next smaller integer (to the left of the x-value on a number line).
Examples: (1, 1) , (-3, -3), (1.5, 1), (-2.4, -3)
(Notice how this function works with negative x-values.)
Greatest Integer Function notation: y = [ x ].
The graph is shown at the right. |
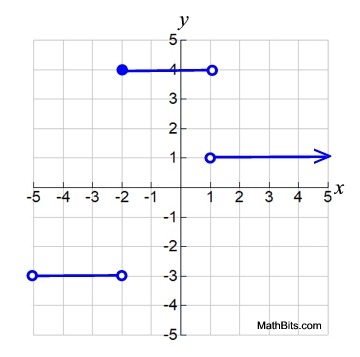
Since no restrictions are placed on the domain,
it is assumed that all possible values will be used.
Domain of entire function: All Real Numbers
Range of entire function: All Integers
|
Notice the truly accurate "stair" appearance of this specific step function.
All of the line segments are of equal length and are the same vertical distance apart.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


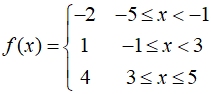
 Domain of entire function: [-5,5] or -5 < x < 5
Domain of entire function: [-5,5] or -5 < x < 5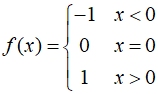
 Domain of entire function: All Real Numbers
Domain of entire function: All Real Numbers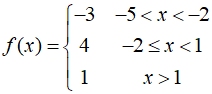
 Domain of entire function:
Domain of entire function: 