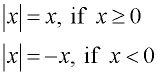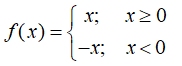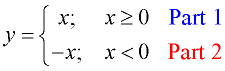|
One of the functions that falls under the category of a piecewise-defined function is the Absolute Value Function.
The absolute value of a number is the distance between the number and zero on a real number line. Since distance is a positive concept (or zero), absolute value is never negative.
| 8 | = 8 | -6 | = 6 |
 |
While the absolute value function can be written as a single statement, y = | x | or f (x) = | x |,
we have seen, by its definition, that the function is actually composed of two linear "pieces".
When graphing functions, remember that y = f (x), allowing for either "y" or "f (x)" to represent the function.
Our original definition
of Absolute Value:
 |
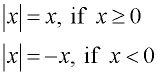Piecewise definition
of Absolute Value
f (x) = | x |
 |
|
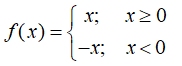 Seeing Absolute Value Function as a Piecewise Function: |
Since the definition of the absolute value function is stated in two parts, we can think of the graph of the absolute value function as a piecewise function, composed of two linear "pieces".
Piecewise definition
of Absolute Value
y = | x |
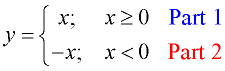
We know the important "point" for this graph
is x = 0 with the coordinates (0,0).
To graph Part 1: For y = x, the slope m = 1 and the y-intercept is 0.
Graph the ray to the right of (0,0).
Closed circle at (0,0).
To graph Part 2: For y = -x, the slope m = -1 and the y-intercept is 0.
Graph the ray to the left of (0,0).
Open circle at (0,0).
|
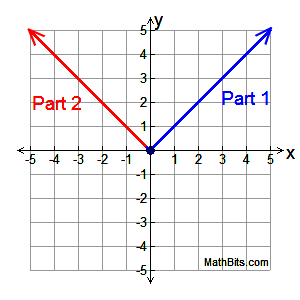
Absolute Value, f (x) = | x |,
is a piecewise function.
Domain for entire function: All real numbers
Range for entire function: y > 0
|
| Visible Features of the Absolute Value Function: |
The Absolute Value (including transformations of the function) usually have a
recognizable " V-shape", with the "V" being up-right or up-side-down.
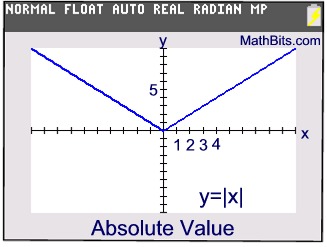
y = | x | creates y-values that are positive or zero.
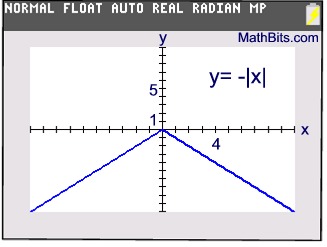
y = -| x | creates y-values that are negative or zero.
Notice that the graph of y = | x | is symmetric with respect to the vertical y-axis.
Also, the graph of y = -| x | is symmetric with the y-axis.
(symmetric = mirror images)
|
| |
 |
 |
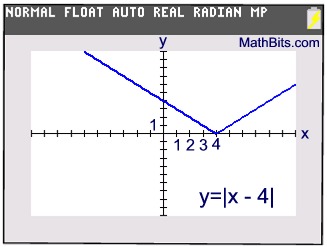
Transformations applied to the Absolute Value function will alter its position.
Subtracting 4 from x moves the absolute value
graph horizontally 4 units to the right. The
y-values remain positive or zero. |
|
| Examining Coefficients: |
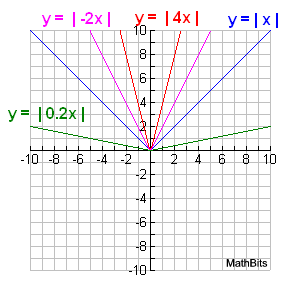
What effect do coefficients have on the absolute value function, y = | x | ?
 |
Some coefficient observations:
• As the coefficient of x gets larger, the width of the graph becomes thinner, bringing the graph closer to its line of symmetry.
• As the coefficient of x gets smaller, the width of the graph becomes broader, taking it farther from its line of symmetry.
Note: The coefficient of x lies inside the absolute value bars. |
• In this situation, if the coefficient of x is negative, the graph is the same as if that coefficient were positive. The coefficient is acted upon by the absolute value property of multiplication:
| a • b | = | a | • | b |
| -2 x | = | -2 | • | x | = 2 • | x | = | 2 | • | x | = | 2x |
So, y = | -2x | is the same as y = | 2x |
|
 |
On the TI-84+ family of calculators,
to graph absolute value,
go MATH, arrow right to NUM, choice 1 abs(.
On other calculators, look for "abs"
to represent absolute value.
|
|
FYI: Other terms associated with "absolue value" are magnitude and modulus.
Magnitude (or absolute value) is the positive measurement of a quantity, or the size of the quantity. Magnitude can refer to the length of a vector.
Modulus (or absolute value) is the term used for absolute value in complex analysis, and can also refer to the magnitude of a vector.
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
