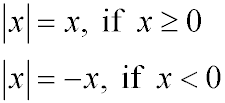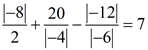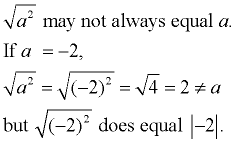|
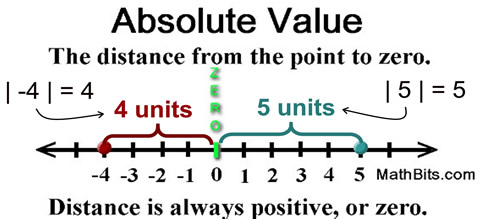
The absolute value of a number is the distance between the number and zero on the real number line. Distances are measured as positive units (or zero units). Consequently, absolute value is never negative. Absolute value answers the question "How far from zero?", but not the question "In which direction from zero?". The notation used for absolute value is two vertical bars.

Algebraically speaking,
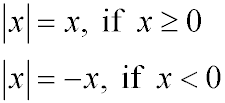 |
It is understood that finding the absolute value of a quantity will yield a positive result (or zero). But that "quantity" with which you are working may be a positive or negative number. So, when you see | x |, do not assume x is positive. While the result is positive, the x-value could be negative.
If x = 5, then | 5 | = 5.
Both x and the absolute value of x are positive.
If x = -8, then | -8 | = 8.
While x is negative, the absolute value is positive. |
 Examples: Examples: |
1. | − 3 | = 3 |
2. − | − 7 | = − 7 |
| |
3. | 0 | = 0 |
4. | − 5 |2 = 25 |
| |
5. − | (− 8)2 | = − 64 |
6. − | − 3 |2 = − 9 |
| |
7. | 3 | + | − 7 | − | − 2 | = 8 |
8. | − 8 | + ( − 9) + | − 14 | + ( − 2) = 11 |
| |
9. 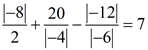 |
10. | − 3 + 6 |2 + | − 3 | = 12 |
 Things to Consider: Things to Consider:
Measuring Distance:
| 8 − 3 | = 5 and | 3 − 8 | = 5
The expression | a − b | represents the distance from a to b on the number line.
This distance is the same when measured forward from 3 to 8, or backward from 8 to 3.
|
Properties when Dealing with Absolute Value:
| 3 x 7 | = | 3 | x | 7 | (True)
When working with operations under absolute value, what is true and what is not true?
| 1. Multiply |
| a • b | = | a | • | b | |
True |
| 2. Divide |
| a / b | = | a | / | b | |
True |
| 3. Add |
| a + b | ≠ | a | + | b | |
False |
| 4. Subtract |
| a - b | ≠ | a | - | b | |
False |
| 5. Power |
| an | = | a |n |
True |
| 6. Inequality |
| a + b | < | a | + | b |
(called the Triangle Inequality) |
True |
|
Square Root Definition:
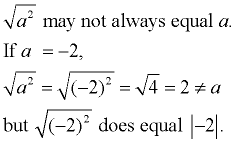 |
|
For help with absolute value
on your calculator,
click here. |
|
For graphing information on Absolute Value, see Absolute Value Function.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|