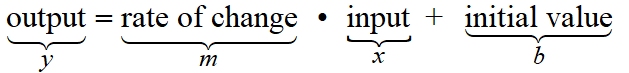|
Linear functions can be used as models for many real-world situations. While any form representing the equation of a line can be used, the form y = mx + b is the most popular.
For a linear model, "y" represents the output and "x" represents the input.
 |
When setting up a linear model, such as y = mx + b, you are dealing with two key components: the slope, m, and the y-intercept, b.
You will need to determine these two key components
from the problem in order to set up a linear model.
• slope, m: the rate of change, how fast something is changing
• y-intercept, b: an "initial condition", the starting amount at x = 0.
|
|
When modeling word problems, it is may be helpful to think about y = mx + b in "words":
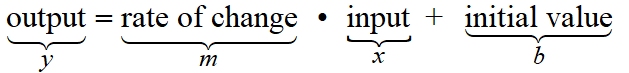
output = dependent variable and
input = independent variable

| Let's take a look at some things you will be expected to do when "modeling": |
Don't be alarmed that the problem may be using variables other than "x" and "y".
It will be important, however, to specify, in your solution, what the variables you are using represent.
You will be expected to "identify your variables",
if the variables are not already specified in the problem. |

When dealing with word problems,
you
need to label your answers when appropriate.
For example, when asked to state the "rate of change", the answer should be labeled:
"gallons per minute", or
"miles per hour", or "population per year" or "increases per gram".
You will be expected to "label" answers where appropriate. |

Remember that word problems require "limitations" be set on function equations,
since ± infinity is seldom a viable solution to a word problem.
Be sure to specify the domain for any function you list as an answer.
You will be expected to "state the domain" on any functional
equation you supply as an answer. Think "limitations". |

If a question asks you to prepare a graph, be sure to include all of the details that make a graph complete (labeled axes, labeled scale on both axes, accurately drawn line).
Now, is not the time for a rough sketch.
You will be expected to "properly prepare a graph".
If asked to graph the function, prepare a well labeled graph. |

While model questions contain a written explanation of the situation,
the questions may also include tables, charts, drawings and/or graphs.
Read carefully and examine all of the information given in the problem!
You will be expected to "read carefully".
Pay attention to any charts, diagrams, and/or graphs
associated with the problem. |

Check out Modeling problems.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|