|
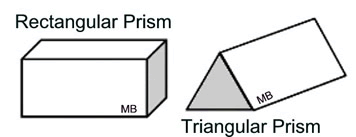
Prisms are three-dimensional closed surfaces.
At this level, the focus will be on right rectangular prisms and right triangular prisms.
|
A prism is a three-dimensional solid figure with two parallel faces (ends), called bases, that are identical (congruent), and lateral flat faces which are rectangles.
|
|
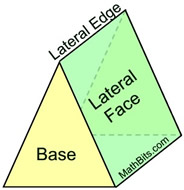 Right Triangular Prism
Right Triangular Prism
|
Regarding right prisms:
• |
The bases (ends) are parallel and identical (congruent). |
• |
The lateral (flat) faces are rectangles. |
• |
Prisms are named for the shape of the bases. |
• |
Prisms do NOT always sit on their bases
|
• |
All of the prisms, at this level, are right prisms. |
• |
Prisms are called polyhedra since their faces are polygons. |
|
The following diagrams show various prisms with their bases shaded.
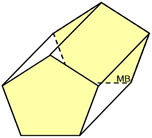 Right Pentagonal Prism
Right Pentagonal Prism |
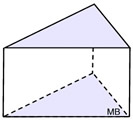 Right Triangular Prism
Right Triangular Prism |
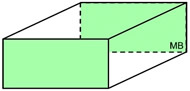 Right Rectangular Prism
Right Rectangular Prism |
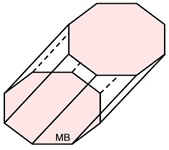 Oblique Octagonal Prism
Oblique Octagonal Prism |
• All prisms discussed here will be right prisms.
• In a right prism, the identical bases (ends) will appear directly above
one another
when the prism is sitting on its base.
(They will not look like they are slanted or going to fall over
as does the oblique octagonal prism above.
Oblique prisms are prisms that are not "right" prisms.)
.

|
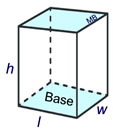
The right rectangular prism may be the most recognizable prism, because it looks like a "box".
If all of the faces in a right rectangular prism are identical squares (since a square is a special case of a rectangle), the solid is called a cube. |
|

Volume of a Prism:
(also see Volume)
For a right rectangular prism:
A common formula for volume of a 3D "box" is:
Volume = length x width x height:
V = l • w • h
 V = l • w • h
V = l • w • h or V = B • h
(B = area of the base)
|
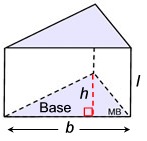
For a right triangular prism:
Since the base is always a triangle, you may see the volume formula stated as:
Volume = ½ base x height x length:
V = ½ • b • h • l
 V = ½ • b • h • l or V = B • h
V = ½ • b • h • l or V = B • h
(B = area of the base)
|
In the formulas above, you can see the area of the base is part of the volume formulas:
V = l • w • h where A = l • w is the area of a rectangle.
V = ½ • b • h • l where A = ½ • b • h is the area of a triangle.
(Unfortunately, using this right triangular prism formula can be a bit confusing because
"h" is the height of the triangular base and "l" is the height of the prism. But,
in the formula for the right rectangular prism, "h" is the height of the prism.)

Volume formula for ALL prisms:
A more general formula for the area of ALL prisms is:
Volume = (the area of the base) x height: V = B • h
where B = the area of the base of the prism and h = height of the prism.
The volume of a prism is its base area times its height. Vprism = Bh |
V = volume in cubic units; B = area of the base in square units; h = height of prism in units
The surface area of a prism is the sum of the areas of the bases plus the areas of the lateral faces. (The sum of the areas of all the faces.) |
|
When dealing with surface area, it is helpful to work with a net of the figure,
as the net allows for all of the faces to be clearly seen.
|
A net is a two-dimensional "pattern" that can be folded to form a three-dimensional solid. It is a "pattern" of the layout of a three-dimensional solid showing each of its faces. |
|
Example:
Find the surface area, SA, of the right triangular prism shown at the right.
|
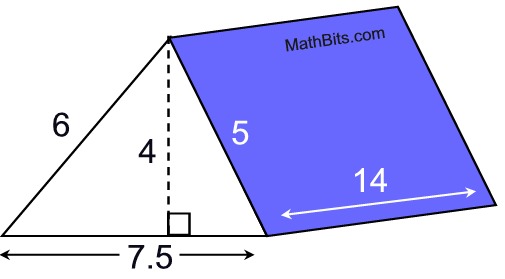
Actual measurements have been rounded to nearest tenth.
|
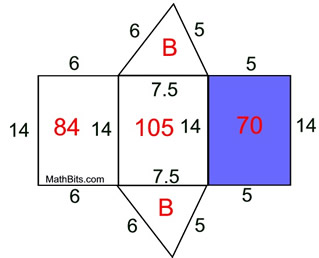
Solution (using a net):
• Prepare a net, as shown.
• Find the area of the triangular base.
Since the base is a triangle, the A = ½ b• h.
area of Base = ½ • 7.5 • 4 = 15 sq. units.
• Find areas of the 3 rectangular lateral faces. 84, 105, 70
• Add the areas of all of the faces.
Remember that there are two Bases.
SA = 15 + 15 + 84 + 105 + 70
= 289 square units |
 |
|
Notice how a net made the computation of the surface area easy to organize.
A net of this prism shows the "surfaces" whose areas, when added, comprise the surface area.
The red values represent areas of the sections.
In this example, B = area of the prism's base
= ½ (triangle's base) • (triangle's height).
Adding all of these sections together will yield the surface area of the solid.

FYI: The work that was done in the example above can be combined to reveal
a "formula" for the surface area of a right prism.
B = area of the base
SA = 15 + 15 + 6•14 + 7.5•14 + 5•14
= 2(16) + (6 + 7.5 + 5)•14
= 2(B) + (base perimeter) • height
The surface area, SA, of a right prism can be found
using the formula:
SA = 2B + ph
B = area of base, p = perimeter of base, h = height. |

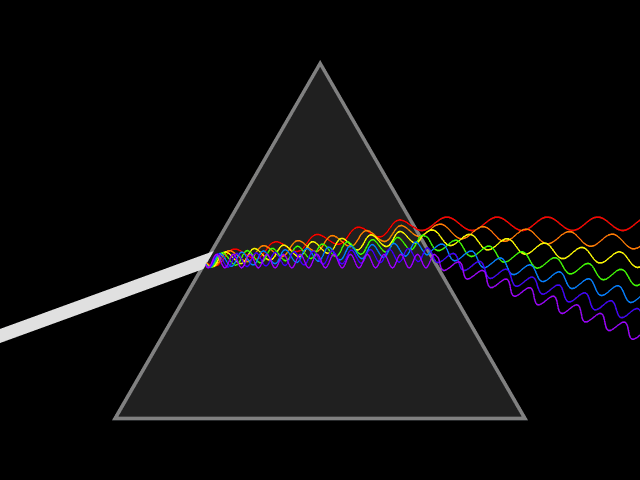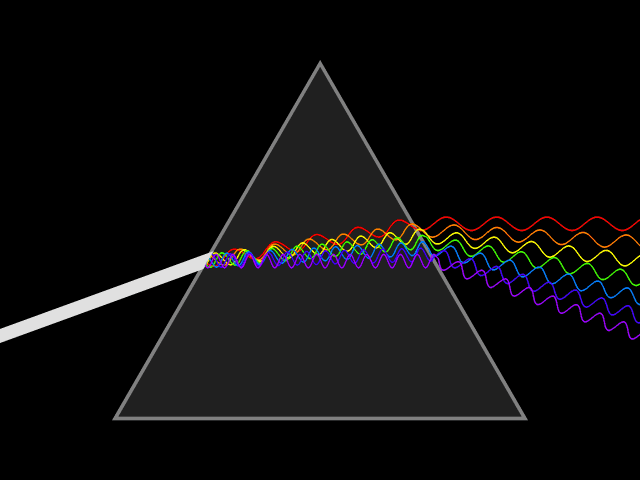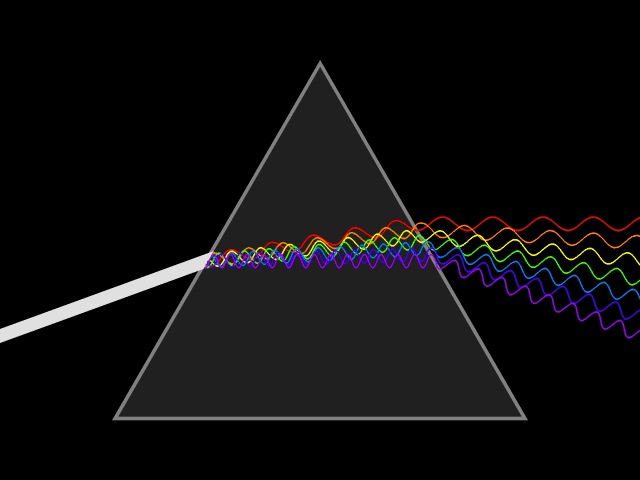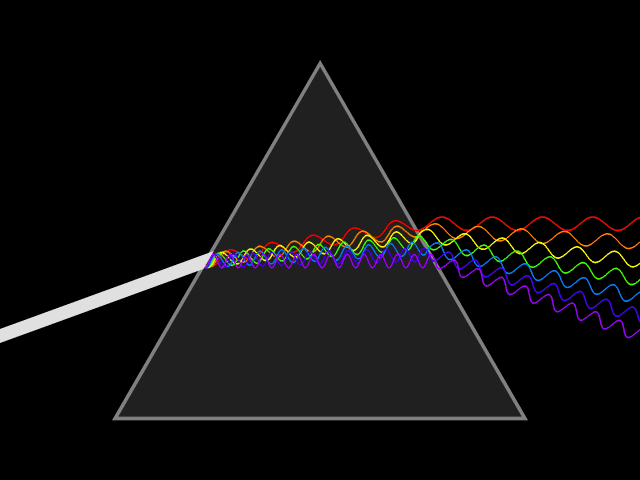
In the Real World:
Reflective Prisms
In the study of optics, prisms are used to reflect light, such as occurs in binoculars. Prisms are also used to disperse light, or break light into its spectral colors of the rainbow. The most commonly used optic prism is a triangular prism, which has a triangular base and rectangular sides. |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|