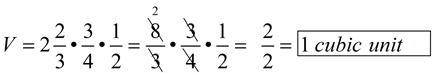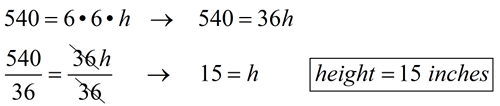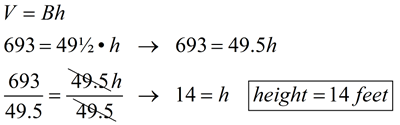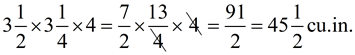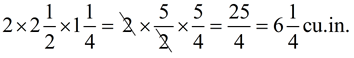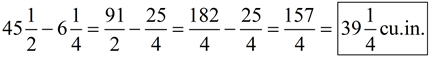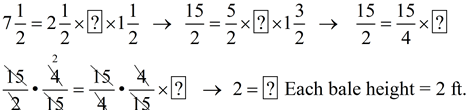|
Right Rectangular Prisms (Boxes)
Volume is measured in cubic units.
1 cubic foot =
1728 cubic inches
(a cubic foot is
1 ft. by 1 ft. by 1 ft.
which is also
12 in. by 12 in. by 12 in.) |
 |
1 cubic yard
= 27 cubic feet
(a cubic yard is
1 yd. by 1 yd. by 1 yd.
which is also
3 ft. by 3 ft. by 3 ft.) |
Volume of a Right Rectangular Prism |
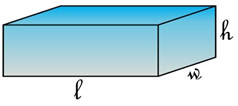
The volume of a right rectangular prism (a box), where l = length, w = width, and h = height, is :
V = l • w • h = lwh
V = volume in cubic units |
 |
The General Formula for ALL prisms is:
The volume of a prism is the area of its base times the prism's height.
Vprism = Bh
|
|
V = volume in cubic units; B = area of the base in square units; h = prism's height in units

 (Using Fractional Sides) (Using Fractional Sides)
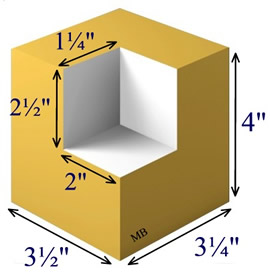
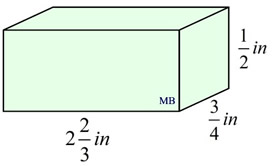
1. Find the volume of the right rectangular prism shown at the right.
Remember to show your work. State your final answer labeled with the appropriate units.
Solution: V = lwh
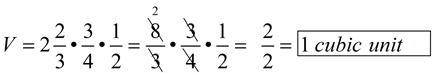 |
 |

 (Find Missing Height) (Find Missing Height)
2. A right rectangular prism has a square base with a side length of 6 inches. The volume of the prism is 540 cubic inches. Find the height of the prism, in inches.
Remember to show your work.
Solution: V = lwh (where V = 540, l = 6 and w = 6)
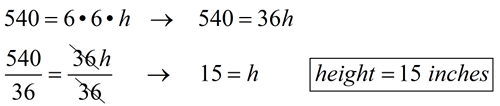 |
|

 (Using Decimal Sides) (Using Decimal Sides)
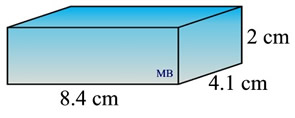
3. Find the volume of the right rectangular prism shown at the right.
Remember to show your work.
Solution: V = lwh 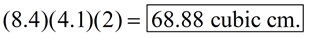 |
|

 (Using General Formula for Prisms) (Using General Formula for Prisms)
3. A right rectangular prism has a base with an area 49½ square feet, and a volume of 693 cubic feet. What is the height, in feet, of this prism?
Remember to show your work.
Solution: We do not know the length or width of this prism. We cannot assume the base is a square. We need to use the general formula for volume of prisms: V = Bh (where B = area of the base (which we know), and h = prism's height).
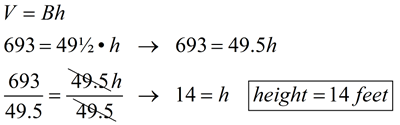
|
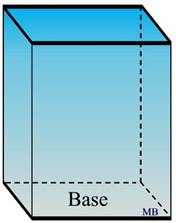 This problem needs to use the general formula for the volume of prisms, since you have no way of knowing the length or width of this prism.
This problem needs to use the general formula for the volume of prisms, since you have no way of knowing the length or width of this prism. |

 (Applied Use - Cut Out) (Applied Use - Cut Out) 
 (Applied Use - Stacking) (Applied Use - Stacking)
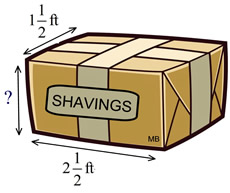
5. Wood shaving used as bedding for small animals is packed as "bales" in the form of right rectangular prisms. The dimensions are as shown at the right. The volume of one "bale" is 7½ cubic feet. If three bales are stacked on top of one another, what is the height, in feet, of the stacked bales?
Remember to show your work.
Solution: Find the missing height.
V = lwh
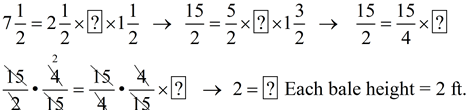
If each bale is 2 feet in height, a stack of 3 bales will have a total height of 6 feet. |
Stacked Bales
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|