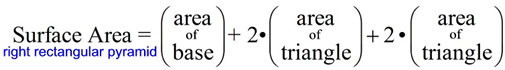|
Surface area is the total area that the surface of a three-dimensional object occupies, in square units. |
|
Surface area is like the wrapping paper you put on a gift (without overlapping). To find the surface area, you need to find the amount of wrapping paper needed to cover (exactly) each face of a solid. |
|

Surface Area using a Net: |
|
Surface area is the sum of the areas of all of the polygonal faces of a solid.
Surface area is labeled in "
square units".
A "net" is a two-dimensional shape that can be folded to form a three dimensional shape or solid. A net is the pattern formed when a 3-D solid is laid out flat, showing each face of the solid.
A "net" is a valuable aid in working with surface area.
The advantage of examining the net is that you can see each of the faces of the figure,
making computing the surface area easier.

Find the surface area
of this prism.
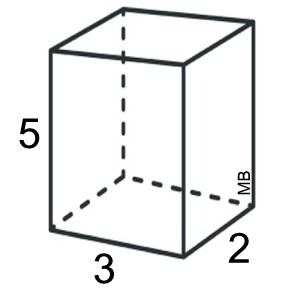 Finding the surface area means finding the area of EVERY
Finding the surface area means finding the area of EVERY
one of the 6 faces and adding these results.
|
If you cut apart this box and flatten out the pieces, you will get a shape, called a net, similar to the one at the right.
Several options are possible.
What we know about this net:
1. There are 6 rectangular faces.
2. There are 3 sets of rectangles of equal measures (3 by 2, 3 by 5, and 2 by 5).
3. There are right angles in the corners.
4. The area of all 6 shapes can be found by the formula
A = bh.
|
Net:
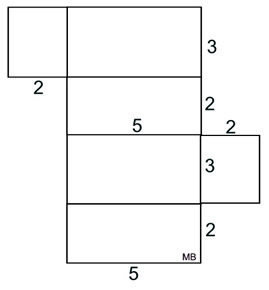 |
| The surface area of this right rectangular prism is the sum of the areas of all 6 shapes in the net. Surface Area = 2•(3•5) + 2•(3•2) +2• (5•2) = 62 square units. |
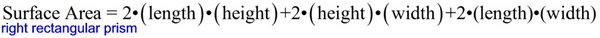
SA = 2lh + 2hw + 2lw
where SA = surface area, l = length, h = height, w = width

Find the surface area
of this
right
triangular prism.
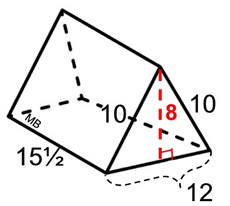 The base triangles in this example are isosceles (both have legs of 10). The base triangles may not always be isosceles.
The base triangles in this example are isosceles (both have legs of 10). The base triangles may not always be isosceles. |
What we know about this net:
1. There are 5 faces.
2. There are 2 congruent rectangles (10 by 15½).
3. There is 1 rectangle
(12 by 15½)
4. The bases (Δs) are congruent.
5. The needed formulas are:
rectangles: A = bh
triangles: A = ½ bh
|
Net: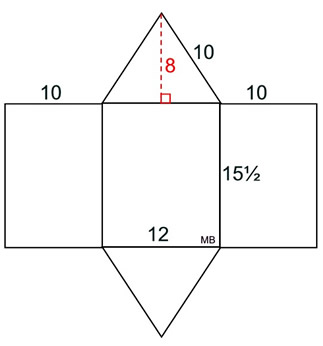 |
The surface area of this right triangular prism is the sum of the areas of all 5 shapes in the net.
Surface Area = 2•(½(8•12)) + (10•15½) + (10•15½) + (12•15½) = 592 square units. |


Right Rectangular Pyramid |
|
Find the surface area
of this
right
rectangular pyramid.
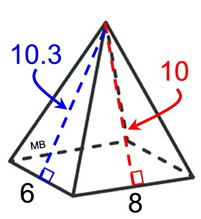 Actual dimensions have been rounded to nearest tenth.
Actual dimensions have been rounded to nearest tenth. |
What we know about this net:
1. There are 5 faces.
2. There is one rectangle base.
3. There are 2 sets of congruent triangles.
4. The given heights are the heights of the lateral faces, not the height of the pyramid.
5. The needed formulas are:
rectangle: A = bh
triangles: A = ½ bh
|
Net:
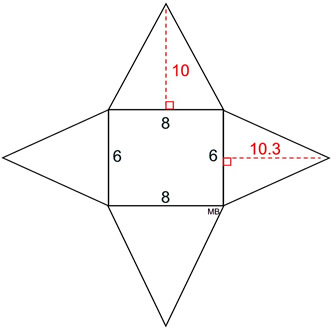 |
The surface area of this right triangular prism is the sum of the areas of all 5 shapes in the net.
Surface Area = (8 • 6) + 2 • ½ • (8 • 10) + 2 • ½ • (6 • 10.3) = 189.8 square units.
|
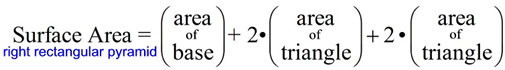



Alternate Unwrapping - Nets: |
A 3-D shape may have more than one possible "net".
Here are a two examples of alternative "un-wrappings" to form nets.

Working with different units: |
When solving real world problems related to surface area,
you may be asked to
convert a measurement from square feet to square inches.
1 square foot = 144 square inches
(a square foot is 1 ft. by 1 ft.
which is also 12 in. by 12 in. = 144 sq.in.)