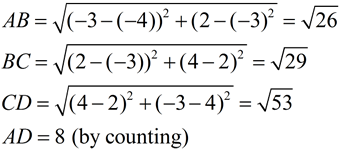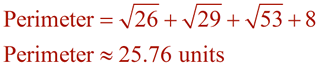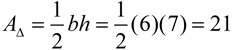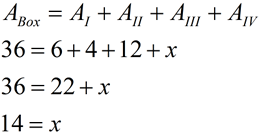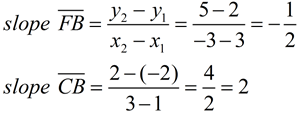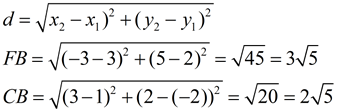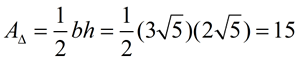|
If the sides of a polygon lie on the grids of the graph paper (horizontal or vertical), the lengths of the sides of the polygon can be found by simply counting. You have used this counting method in the past to find such lengths.
Unfortunately, not all polygons are positioned so their sides lie on the grids of the graph paper. When this happens we need to use more sophisticated techniques to find the lengths of the sides.
If the sides of the polygon lie on the grids of the graph paper (horizontal or vertical), counting will yield the side lengths of the polygon.
If the sides do NOT lie on the grids of the graph paper, the Distance Formula will find the lengths of the sides.
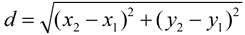
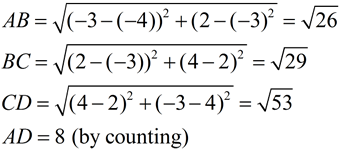
|
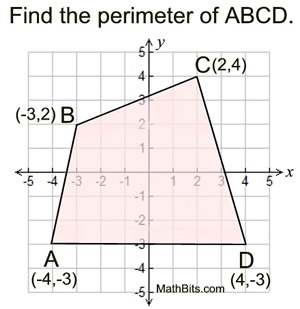
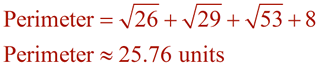
Only round your answer if told to do so.
Otherwise, given the "exact" answer.
|

When finding the area of a polygon positioned on the coordinate axes, first look to see if the needed segments (such as the base and the height to that base) lie on the grids of the graph paper. If they do, you may be able to find the area by counting.
It is unlikely, however, that this will always be the case at this level of study.
|
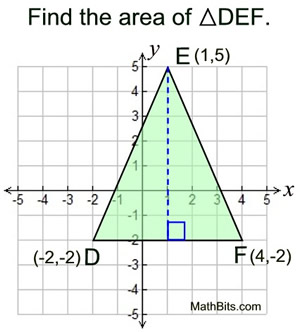
In this triangle, the base and the height to that base lie on the grids of the graph paper. Simply "count" these lengths and use the formula for the area of a triangle.
DF = 6 (by counting)
The altitude from E = 7 (by counting)
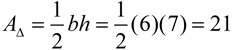
The answer is 21 square units.
Unfortunately, not all problems are this easy.
|
|
|
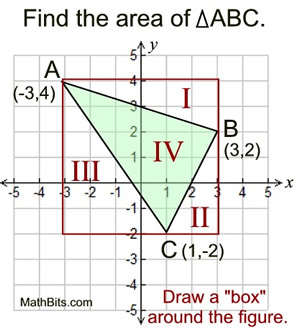
When the needed segments do NOT lie on the grids of the graph paper, an old friend, referred to as the "Box Method", will come to your rescue.
The box method is simple, easy to calculate, and works for all polygons drawn on a coordinate axes.
The box method is based upon the concept that "The whole is equal to the sum of its parts." The box is subdivided (decomposed) into its parts, one of which is the figure whose area you are trying to calculate.
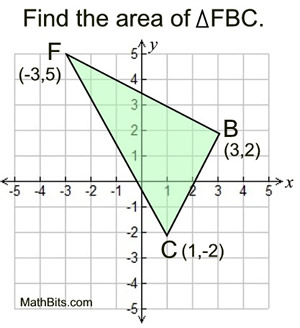
As the example at the right shows, once the box is drawn, all lengths relating to the box can be counted, except for those in ΔABC.
Read more about this method at Box Method.
|
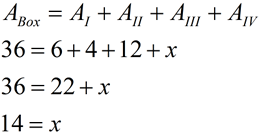
The answer is 14 square units.
|

In certain situations, it may be possible to calculate the area of the figure by verifying a perpendicular and using the Distance Formula.
|
You may think that ΔABC, in the previous example, is a right triangle, but it is NOT a right triangle. If, however, we change the coordinates of vertex A, right ΔFBC is created. This can be verified by calculating the slope of the legs of the triangle.
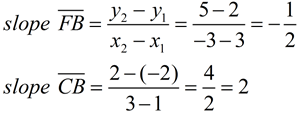
Since the slopes are negative reciprocals of one another, the legs are perpendicular, giving a right angle at B.
Now, apply the Distance Formula to find the lengths of the legs and use the area formula for a triangle.
|
|

In the section on Equations, we will examine a more elaborate algebraic method of finding area on a coordinate axes using slopes and equations of lines.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|