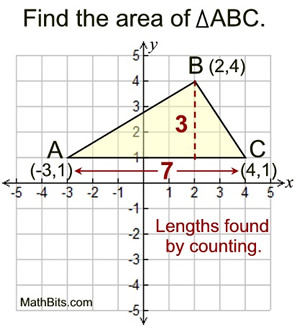
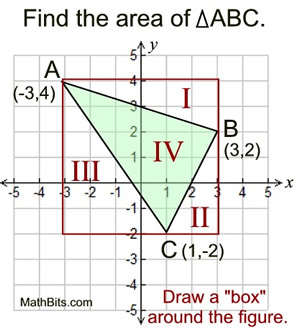
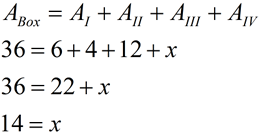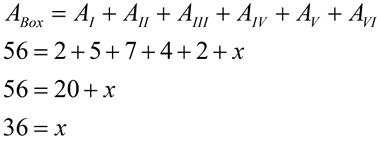GeometrySmallLogo

Box Method - Area on a Coordinate Grid
 MathBitsNotebook.com

Topical Outline | Geometry Outline | MathBits' Teacher Resources

Terms of Use   Contact Person: Donna Roberts
divider
refresher
We are going to see that finding the area of polygons drawn on a coordinate axis can be an easy process by using a simple box. Whether the box is needed, depends upon the placement of the polygon on the coordinate grid. Two situations are possible:
Sides are parallel to the axes:
If the polygon is drawn such that its sides (or needed segments) lie ON the grids of the graph paper, COUNT the lengths and use the appropriate area formula.
Sides are NOT parallel to the axes:
If the polygon is drawn such that its sides (or needed segments) do NOT lie ON the grids of the graph paper, draw a "BOX" around the polygon to determine the area.


Sides are parallel to the axes:


COUNT to find the needed lengths.
The base of the triangle lies ON the grids of the graph paper (horizontal), and the altitude (vertical height) also lies ON the grids of the graph paper, since it is perpendicular to the base.

By counting, the base length is 7 units and the altitude is 3 units.
Use the area of a triangle formula:
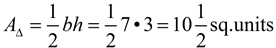
boxmath1
The answer is 10½ square units.

AC can also be found by subtracting the x-coordinates of the two points (4 - (-3) = 7). Since the base of the altitude is located at (2,1), the altitude can be found by subtracting the y-coordinates (4 - 1 = 3).


box1
To COUNT: stand at A and take one step
to the right to the next grid line. Continue
stepping and counting until you reach C.
divider
Sides are NOT parallel to the axes:



The sides of this ΔABC do NOT lie on the grid lines of the graph paper. Use the "Box Method" to solve for the area of the triangle.

• Draw the smallest "box" possible to enclose the polygon (ΔABC). Be sure that the "box" follows the grids of the graph paper.

• Number each of the parts of the box with a Roman numeral (ignore the axes when numbering).

• "The whole is equal to the sum of its parts." The area of each of the parts of the "box" added together equals the area of the "box".
boxarea2
The answer is 14 square units.


box2

Note:
* Find the area of the box by counting.
* Represent the triangle you need by x.
* Find the area of each of the right triangles by counting and using the formula for the area of a triangle.

divider

Dealing with odd shaped pieces:


There are times when the "box" will not form nice right triangles in each of the corners, as shown here in the upper left corner. In such a case, it is necessary to further subdivide these sections into one rectangle and two right triangles, so the lengths can be easily counted.
boxmath2
The answer is 36 square units.

box3a
Remember to keep your work simple by always forming shapes around the figure that are easy to count.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Use".