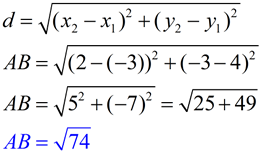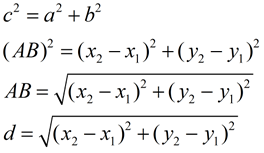|
Finding the lengths of line segments (or distance) on coordinate axes
can be accomplished in three basic ways.

When line segments on the coordinate axes are vertical or horizontal, their lengths (or the distance) can be found by counting.
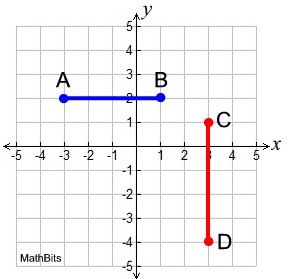
Example 1: Given the graph at the right, find AB and CD.
Solution: Since these segments follow the grids of the coordinate axes, their lengths can be found simply by counting.
AB = 4 units (by counting).
CD = 5 units (by counting).
|
|
This method does NOT work for segments placed diagonally across the grid.

|

When line segments are diagonally placed, right triangles and the Pythagorean Theorem can be used to find their lengths (or distances).
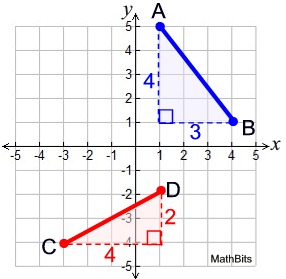
Example 2: Given the graph at the right, find AB and CD.
Solution: Using the perpendicular nature of the grid lines, you can draw a right triangle with the line segment as its hypotenuse. Count the vertical and horizontal sides of the Δ, and use the Pythagorean Theorem to find the hypotenuse (the segment).
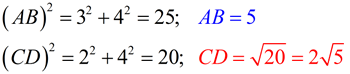 |
|

If you examine "how" the Pythagorean Theorem is working in Method 2,
you will find that there is a pattern at work, which we call the Distance Formula.
We will develop this pattern after Method 3.
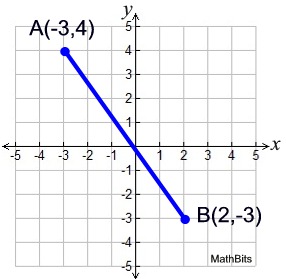
 Example 3: Given the graph at the right, find AB. Example 3: Given the graph at the right, find AB.
Solution: The advantage of using the Distance Formula is that you do not need to draw a right triangle to find the answer. All you need to know are the coordinates of the endpoints of the segment.
Let A be (x1, y1) and B be (x2, y2).
It does not matter which point is used first, but if you choose -3 to be x1, then you must choose its partner, 4, to be y1.
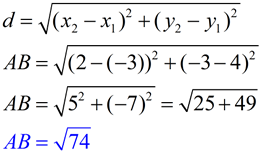 |
The Distance Formula can be used to find the lengths of all forms of line segments: horizontal, vertical and diagonal.
|
|

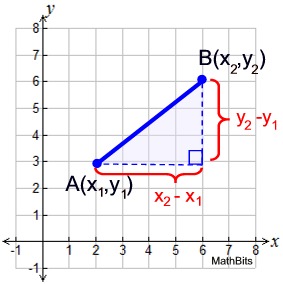
• Start by drawing a right triangle anywhere on a coordinate axes. We will be using the first quadrant for clarity. Draw the Δ so the legs lie on the grids of the graph paper.
• Label the endpoints of the hypotenuse as A(x1, y1) and B(x2, y2).
• Represent the lengths of the legs of the right triangle as the difference of the x and y coordinate values.
• Apply the Pythagorean Theorem.
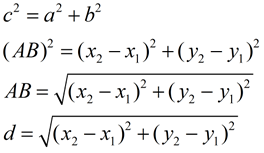
|
 Keep in mind that the line segment could be placed in any quadrant. As such, the values of Keep in mind that the line segment could be placed in any quadrant. As such, the values of
(x2 - x1) and (y2- y1), which represent the lengths of segments, are theoretically positive (absolute values) and may be written as
|x2 - x1| and |y2- y1|.
This issue of absolute value will not be a concern in the Distance Formula since these values are being squared, thus creating positive values.
|
|
The Distance Formula is a commonly used formula and worth remembering. You should also remember that the Distance Formula is really just a coordinate geometry way of writing the Pythagorean Theorem. If you cannot remember the Distance Formula, you can always draw a graph and use a right triangle and the Pythagorean Theorem to find the numerical segment length. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|



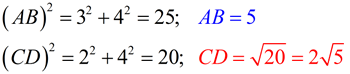
 Example 3: Given the graph at the right, find AB.
Example 3: Given the graph at the right, find AB.