|
 |
Remember -- use your compass
and straightedge only! |
|
 |
You already know how to make these constructions. Just remember the definitions of these terms, and you will have a hint as to how to create their constructions. |
|
By definition, an altitude of a triangle is a segment from any vertex perpendicular to the line containing the opposite side.
The definition tells us that the construction will be a perpendicular from a point off the line. The "point" will be the vertex of the triangle from which the altitude will be drawn, and the "line" will be the side of the triangle to which the altitude will be perpendicular.
Altitude in an Acute Triangle
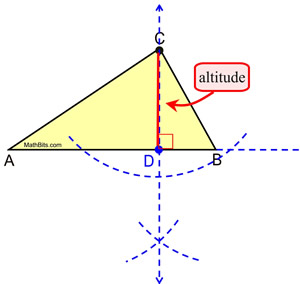 Construct an altitude from vertex C.
Construct an altitude from vertex C.
Notice that it was necessary to extend the side of the
triangle from A through B to intersect with our arc.
The altitude is a segment (not a line), so be
sure to label the portion of the construction that is
actually the altitude, or refer to it by name,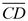 . . |
Altitude in an Obtuse Triangle
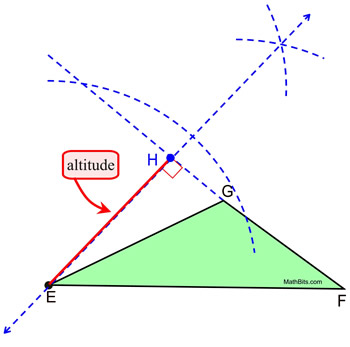 Construct an altitude from vertex E.
Construct an altitude from vertex E.
Notice that it was necessary to extend the side of the
triangle from F through G to intersect with our arc.
Remember, in an obtuse triangle, your altitude
may be outside of the triangle. Be sure to label the
altitude, such as  , or indicate that it
is a segment. , or indicate that it
is a segment. |
By definition, a median of a triangle is a segment joining any vertex of the triangle to the midpoint of the opposite side.
The definition contains the word "midpoint" which tells us that the opposite side will be bisected. We will construct the bisector of the opposite side in the triangle, to locate the midpoint, and then simply connect the midpoint to the vertex to create the median.
Median in an Acute Triangle
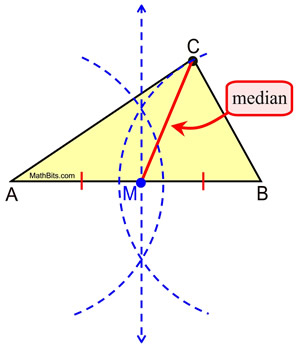 Construct a median from vertex C.
Construct a median from vertex C.
Since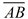 is the side opposite vertex C, we is the side opposite vertex C, we
bisected 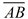 to locate its
midpoint M. Now, to locate its
midpoint M. Now,
simply connect midpoint, M, to
vertex C. |
Median in an Obtuse Triangle
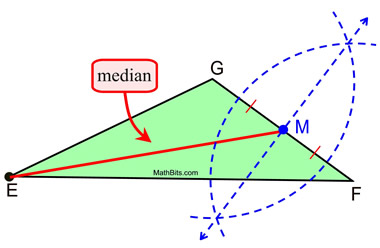 Construct a median from vertex E.
Construct a median from vertex E.
Since  is the side opposite vertex E, we is the side opposite vertex E, we
bisected
 to locate its midpoint, M. Now, to locate its midpoint, M. Now,
simply connect midpoint M to vertex E to create
the median of the triangle.
Remember that the medians of an obtuse triangle
remain inside the triangle (unlike its altitudes). |
Angle Bisector in a Triangle |
By definition, an angle bisector is a ray from the vertex of an angle, into the interior of the angle, forming two congruent angles. Since a triangle contains 3 angles, it will have 3 angle bisectors.
This construction will be a direct application of the construction "bisect an angle".
Angle Bisector
in an Acute Triangle
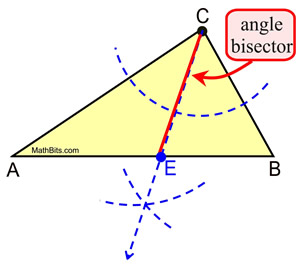 Construct an angle bisector of ∠C.
Construct an angle bisector of ∠C.
When constructing the angle bisector in a triangle,
it is customary to refer to only the portion of the
bisector which lies inside the triangle, such as 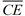 .
Note: an angle bisector does not necessarily
bisect the side of the triangle. We do not know
if AE = EB. We only know that ∠ACE  ∠BCE ∠BCE. |
Angle Bisector
in an Obtuse Triangle
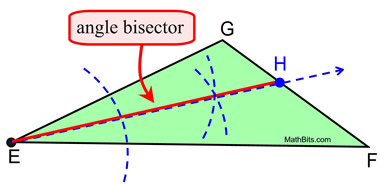
Construct an angle bisector of ∠E.
The angle bisector will be 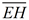 . .
We know that
∠GEH  ∠FEH. ∠FEH.
We do not know if H bisects the side from G to F.
An angle bisector in a triangle is not necessarily
also a median for that triangle. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|







