Bisect an Angle MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Remember -- use your compass and straightedge only!

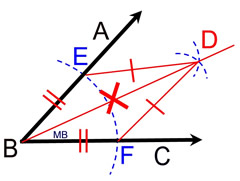
Given: ∠ABC Construction: bisect ∠ABC. Remember that an angle "bisector" will form 2 congruent angles.

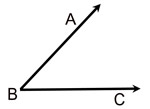STEPS:
1. Place compass point on the vertex of the angle (point B).

2. Stretch the compass to any length that will stay ON the angle.

3. Swing an arc so the pencil crosses both sides (rays) of the given angle. You should now have two intersection points with the sides (rays) of the angle.

4. Place the compass point on one of these new intersection points on the sides of the angle.
If needed, stretch the compass to a sufficient length to place your pencil well into the interior of the angle. Stay between the sides (rays) of the angle. Place an arc in this interior (it is not necessary to cross the sides of the angle).

5. Without changing the span on the compass, place the point of the compass on the other intersection point on the side of the angle and make a similar arc. The two small arcs in the interior of the angle should be intersecting.

6. Connect the vertex of the angle (point B) to this intersection of the two small arcs.
You now have two new angles of equal measure, with each being half of the original given angle.

Proof of Construction: Label the points where the first arc intersects with the sides (rays) of the angle as E and F. The intersection of the two small arcs will be labeled D. Draw 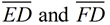. By the construction, BE = BF and ED = FD (length of radii of the same, or congruent, circles). In addition, BD = BD (by the Reflexive Property). All of these equal length segments are also congruent, making ΔBED ΔBFD by SSS. Since CPCTC (corresponding parts of congruent triangles are congruent), we have ∠ABD ∠CBD, showing 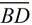bisects ∠ABC, by definition of angle bisector.