 |
Remember -- use your compass
and straightedge only! |
|
Perpendicular from a point OFF a given line. |
|
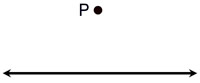
Given: point P off a given line
Construct: a line through P perpendicular to given line.
|
|
STEPS:
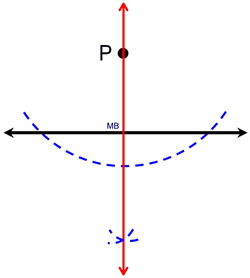
1. Place your compass point on P and swing an arc of any size that crosses the line twice.
2. Place the compass point on one of the two locations where the arc crossed the line and make a small arc below the line (on the side where P is not located). The compass may be increased in length at this point, or it may remain the same length as the first arc made.
3. Without changing the span on the compass, place the compass point on the other location where the first arc crossed the line and make another small arc below the line. The two small arcs should be intersecting (on the side of the line opposite of point P).
4. Using a straightedge, connect the intersection of the two small arcs to point P.
NOTE: If you keep the compass the same length for Step 2, you must place the new arcs on the opposite side of the line, otherwise you will land back on top of point P. If you change the size of the compass for Step 2, you can place the arcs on either side of the line.
|
Does this construction
look familiar?
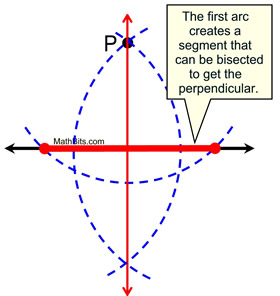
Using perpendicular bisector.
|
|
The construction method shown above on the right can also be applied to the construction where P is located ON the line.

Proof of Construction: (for this proof, the arcs made, following the first arc, will be of an extended length)
Label the construction: A and B are the points of intersection with the first arc, C is the intersection of the two smaller arcs, and D is the intersection of the perpendicular with the given line. Draw 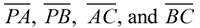 . .
PA = PB and AC = BC since they were constructed as radii of the same circles. These segments are also congruent. Using 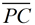 as a common side, ΔPBC is congruent to ΔPAC by SSS. By CPCTC, ∠APC is congruent to ∠BPC. Now, ΔAPD is congruent to ΔBPD by SAS, with common side as a common side, ΔPBC is congruent to ΔPAC by SSS. By CPCTC, ∠APC is congruent to ∠BPC. Now, ΔAPD is congruent to ΔBPD by SAS, with common side 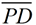 . By CPCTC, ∠PDA is congruent to ∠PDB. These two angles form a linear pair making them supplementary. If two angles are both congruent and supplementary, they are right angles. Consequently, . By CPCTC, ∠PDA is congruent to ∠PDB. These two angles form a linear pair making them supplementary. If two angles are both congruent and supplementary, they are right angles. Consequently, 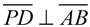 . .
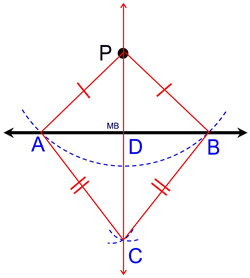
Notice that the quadrilateral APBC is a geometrical "kite".
If the radii had not been lengthened, quadrilateral APBC would be a
geometrical "rhombus", with AP = BP = AC = BC.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|