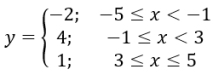|
When we investigated Quadratics, we were introduced to the concept of a "parent function".
For example, the simplest parabola is y = x², whose graph is attached to "Dad" in the graphic at the right.
This graph is known as the "Parent Function" for parabolas, or quadratic functions. All other parabolas, or quadratic functions, can be obtained from this graph by one or more transformations.
Knowing the features of a parent function will be helpful in recognizing the features of transformations, and more complicated graphs. |
 A parent function is the simplest function
of a family of functions.
|
In Algebra 1, we examine a wide range of functions:
constant, linear, quadratic, cubic, exponential, square root, and absolute value functions,
which can all serve as parent functions to generate new familty functions.
Recognizing parent functions will give you a head-start when working with transformations.
Let's take a look at our parent functions, and some of their offspring.
| Parent Function |
Parent Function Graph |
A Child Function Graph |
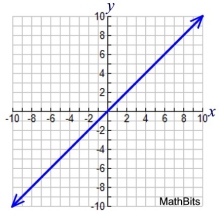
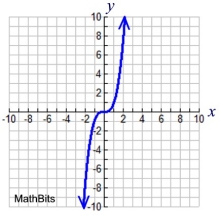
Linear
y = x
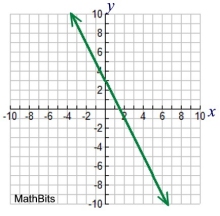
Child: y = -2x + 3
Features:
a straight line
|
 |
 |
The Constant function, y = b, is a linear function whose slope = 0.
It is a "child" of the Linear Function. It is a horizontal line. |
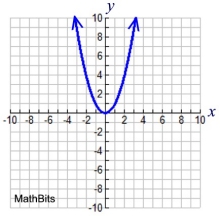
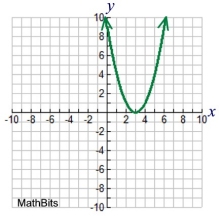
Quadratic
y = x2
Child:
y = x2 - 6x + 9
Features:
parabola U shape
|
 |
 |
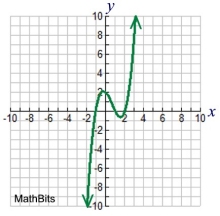
Cubic
y = x3
Child:
y = x3 - 2x2 - x + 2
= (x - 2)(x2 - 1)
Features:
snake-like, crosses x-axis |
 |
 |
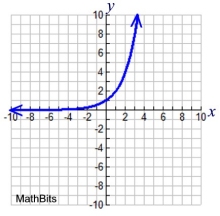
Exponential
y = bx
graphed: y = 2x
Child:
y = (½)x + 2
Features:
horizontal asymptote |
 |
 |
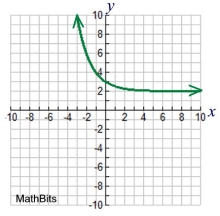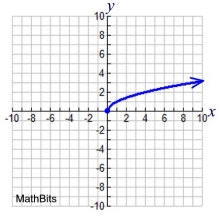
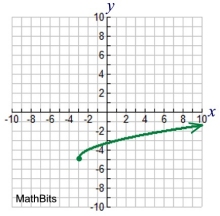
Square Root
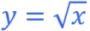
Child:
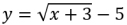
Features:
dot point at one end,
restricted domain
|
 |
 |
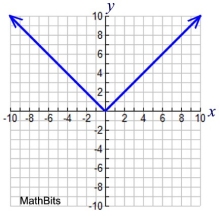
Absolute Value
y = | x |
Child:
y = | x - 2 | - 4
Features:
"V" shape |
 |
 |
Children inherit features from their parents.
Knowing the shapes and features of the parent functions will assist
in understanding the transformations that create their children.
What about piece-wise defined functions and step functions?
Piece-wise defined functions are a combination of two or more equations over a specified domain. They are a "blending" of various functions
where the overall graph is not the direct descendant of only one parent. "Piece-wise" is more of a "format" for expressing the "parts" of the function, rather than the result of a defined "parent".
Step functions are specific piece-wise defined functions in which every piece is a horiszontal line segment (or a point, or a horizontal ray). Like the piece-wise functions, the title "step function" represents a generalizerd "pattern" of finite horizontal linear equations.
They could be "described" as a series of segmented "constant" functions.
But there is not "one" specific defined "parent" step function used to create all other step functions.
There is, however, one specific case of a well known step function that can act as a "parent" that we will investigate in the table below.
| Parent Function |
Parent Function Graph |
A Child Function Graph |
Step Function
(has a "pattern" not a "parent")
Child of the pattern:
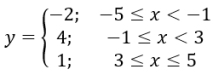
Features:
Finite horizontal (linear) portions; staircase;
in piece-wise format |
No generalized
parent function.
The "pattern" is that
the graph will consist only of horizontal line segments (or a point or ray), appearing at different y-values along the graph.
|
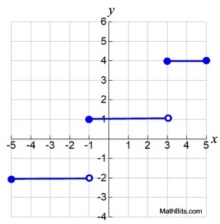
Example of a step function
(not a true "child")
|
Greatest Integer
(a specific "named" step function that is a parent)
y = [ x ]
Child:
y = [ x ] + 2
Features:
equal length, equal height,
staircase appearance |
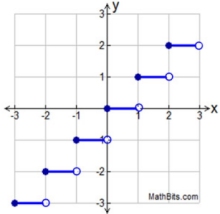
Greatest Integer Function
y = [ x ] |
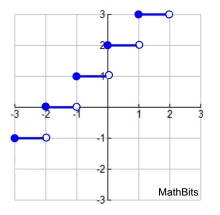
Child: y = [ x ] + 2 |
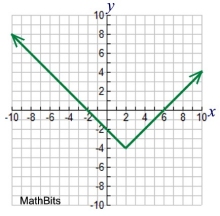
Piece-Wise Defined
(has a "format" not a "parent")
Child of the format:
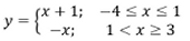
Features:
graph is split into "parts",
continuous or discontinuous
|
No generalized
parent function.
A piecewise-defined function is a function which uses a combination of equations over the intervals of its domain. It is a format for expressing the parts of the function. |
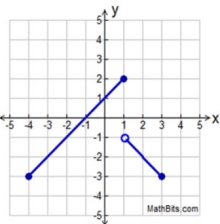 Example of a piece-wise function (not a true "child") |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
