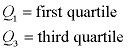|
Knowing the mean, or median, of a data set yields a certain amount of information about the typical data within the set. It is possible, however, that many different data sets may have the same mean value (or median value). To determine how these data sets are different requires that we expand our investigation to obtain more information about the set. One additional investigation is the examination of the measure of spread (or measure of variation) of the data set. How is the data "spread out"?

|
A measure of spread (variability, dispersion, scatter) refers to how the data within the set is "spread out" (or "dispersed", or "scattered") about the mean. |
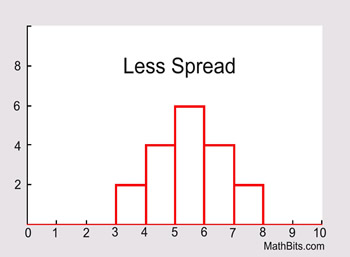
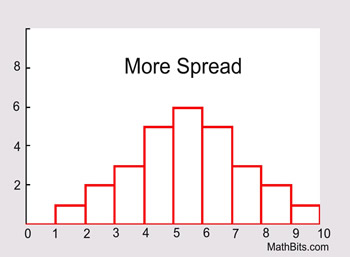
If the data is clustered around the center value, the "spread" is small.
The further the distances of the data values from the center value, the greater the "spread".
While there are a variety of "measures of spread",
at this level we will concentrate on three such measures.
Measures of Spread |
May also be called: Measures of Variability, Measure of Variation,
Measures of Dispersion, or Measures of Scatter
|
|
  Range: Range:
The first method of measuring "spread" of a data set is finding the range. Range is the difference between the largest data value and the smallest data value in the set. While the range is simple to compute, it is often unreliable as a measure of
variability. The range is based on only two values within the set, which may tell very little about "how" the remaining values are distributed in the set. For this reason, range is used as a supplement to other measures of spread, instead of being the only measure of spread.

This range of 43 tells us very little about how the data in this
set is scattered.
The range alone cannot tell us, for example, if the data is clustered to one end of the set,
or if there
is an outlier in the data set. |
|
 Interquartile Range (IQR): (Read more about IQR) Interquartile Range (IQR): (Read more about IQR)
The interquartile range is another form of range which divides the set into four equal parts (or quarters). The three values that form the four divisions are called quartiles: first quartile, Q1; second quartile (median), Q2, and third quartile, Q3. The interquartile range is the difference between the third quartile and the first quartile. You can think of the IQR (also called the midspread or middle fifty) as a "range" between the third and first quartiles. The IQR is considered a more stable statistic than the typical range of a data set, as seen in the first section. The IQR contains 50% of the data, eliminating the influence of outliers.
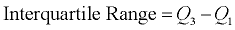 IQR =
8.5 - 3.5 = 5
IQR =
8.5 - 3.5 = 5 |
|
|
|
For calculator help with
IQR from
5 number summary
click here.
|
|
|

For the following method, you need to understand "population" vs "sample" data.
Unlike range and interquartile range, this method utilizes all of the values in a data set to produce a measure of spread. (Not covered in NY NGMS) |
Mean Absolute Deviation (MAD): (Read more about MAD)
The mean absolute deviation is the average (mean) of the absolute value of the differences between each piece of data in the data set and the mean of the set. It measures the average distances between each data element and the mean.
Process:
(1) Find the mean (average) of the set.
(2) Subtract each data value from the mean to find its distance from the mean.
(3) Turn all distances to positive values (take the absolute value).
(4) Add all of the distances.
(5) Divide by the number of pieces of data (for population MAD). |
|

Which methods work best?
Symmetrical data
spread is best summarized by:
MAD |
Skewed data
spread is best summarized by:
range and IQR |
|
Don't ROUND too soon! When working with the formulas for MAD, be careful to avoid rounding too soon. If calculating by hand, always carry more decimal places within the calculations than is expected for the final result. If working with a calculator, carry the full value of the calculator entries until you arrive at the final result.
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|