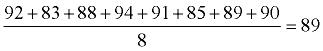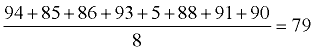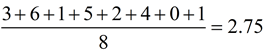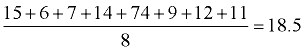|
| |
Let's take a look at some needed vocabulary,
before we begin. |
 |
mean |
(the average) - the sum of all data values divided by the number of the data values. |
deviation |
- the difference between a data value in a set and the mean of the set.
NOTE: the mean (average) of all deviations in a set equals zero. |
absolute value |
- the distance (a positive quantity) of any value on a number line from zero.
NOTE: the sum of the absolute values of deviations on each side of the mean are equal. |
variability |
- refers to how spread out (or clustered together) the values are in a data set.
NOTE: high variability means the data is spread out.
NOTE: low variability means the data is clustered together (close together). |
 |
The Mean Absolute Deviation (MAD) of a set of data is the average distance between each data value and the mean. |
The mean absolute deviation is the "average" of the "positive distances"
of each point from the mean.
The larger the MAD, the greater variability there is in the data (the data is more spread out).
The MAD helps determine whether the set's mean is a useful indicator
of the values within the set. The larger the MAD,
the less relevant is the mean as an indicator of the values within the set.
MAD Process:
(1) Find the mean (average) of the set.
(2) Subtract each data value from the mean to find its distance from the mean.
(3) Turn all distances to positive values (take the absolute value).
(4) Add all of the distances.
(5) Divide by the number of pieces of data (for population MAD).
Steps 4 and 5 are finding the average of the distances. |
Let's compare Sherlock's data set with that belonging to Watson
to see what the Mean Absolute Deviation (MAD) tells us.
|
Sherlock's Data Set:
{92, 83, 88, 94, 91, 85, 89, 90} |
Watson's Data Set:
{94, 85, 86, 93, 5, 88, 91, 90}
|
Find the mean.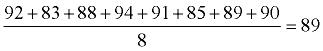 |
Find the mean.
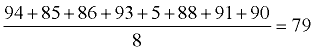 |
Find the difference between each data value and the mean.
92 - 89 = 3
83 - 89 = -6
88 - 89 = -1
94 - 89 = 5
91 - 89 = 2
85 - 89 = -4
89 - 89 = 0
90 - 89 =
1 |
Notice: If you add the positive differences to the negative differences, you get zero. This should always be the case.
3+5+2+0+1=11
-6+(-1)+(-4)=-11
11+(-11) = 0
This also shows that the absolute values of the sums of the differences on either side of the mean are equal. |
|
Find the difference between each data value and the mean.
94 - 79 = 15
85 - 79 = 6
86 - 79 = 7
93 - 79 = 14
5 - 79 = -74
88 - 79 = 9
91 - 79 = 12
90 - 79 = 11 |
Just like in Sherlock's data, the sum of the positive differences and the negative differences is zero.
15+6+7+14+9+12+11 = 74
-74 = -74
74 + (-74) = 0
|
|
Take the absolute value of all of the differences: 3, 6, 1, 5, 2, 4, 0, 1 |
Take the absolute value of all of the differences: 15, 6, 7, 14, 74, 9, 12, 11 |
Find the average (mean) of these absolute values:
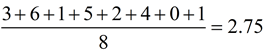 |
Find the average (mean) of these absolute values:
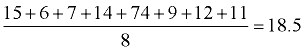 |
Conclusion: The average distance between each data value and the mean is 2.75.
Since the MAD is "small", it implies that the mean of 89 is indicative of the other values within the data set.
83, 85, 88, 89, 90, 91, 92, 94 [mean = 89]
If you were to guess the average grade of this set to be 89, you would have a score which is a reliable indicator of the other scores in this set. The fact that the MAD is small also means that data in the set are close together (clustered). |
Conclusion: The average distance between each data value and the mean is 18.5.
Since the MAD is "large", it implies that the mean of 79 is not a reliable indicator of the other values within the data set.
5, 85, 86, 88, 90, 91, 93, 94 [mean = 79]
If you were to guess the average grade of this set to be 79, you would not have a score which is a reliable indicator of the other scores in this set. The mean in this set is being affected by the outlier score of 5. The large MAD value tells you that the data is widely scattered because of the outlier. |
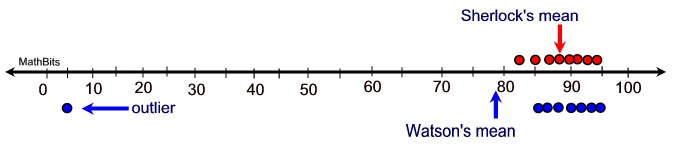
Sherlock's mean of 89 is a good indicator of the grades in his data set. (MAD 2.75 (small) = good indicator)
Watson's mean of 79 is not a good indicator of the grades in his data set.
(MAD 18.5 (larger) = not as good indicator)
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|