 Rationals are the set of numbers, Rationals are the set of numbers, 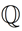 , that are fractions whose numerators and denominators are integers. , that are fractions whose numerators and denominators are integers.
(no denominator is zero) |
|
A rational number is a number that can be expressed as a fraction 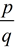 where p and q are integers and q ≠ 0. It is the ratio of two integers. |
You are familiar with rational numbers from your work with fractions.
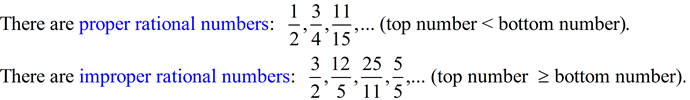

 Rational Numbers can come in various forms: Rational Numbers can come in various forms:
1. We have already seen that fractions are rational numbers.
2. All integers are rational numbers. Since the denominator of any integer can be 1, it is a fraction, making it a rational number.
3. Terminating decimals (2.75 = 2 and 75/100) or repeating decimals (2.333333333...repeating = 7/3) can also be rational numbers.
For example,
1.6 is a rational number because it can be expressed as the fraction 16/10.
4. Since a percent can be changed to a decimal, and most decimals can be changed to fractions, we can say that percents can be considered rational numbers.
For example, 24% = 0.24 = 24/100

 Where are Rationals in the Number System? Where are Rationals in the Number System?
The Rationals contain the set of Integers {..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,...}, the set of Whole Numbers {0, 1, 2, 3, 4, 5, 6, ...} (which includes the set of Natural Numbers {1, 2, 3, 4, 5, 6, ...}), along with the numbers that meet the definition stated above.
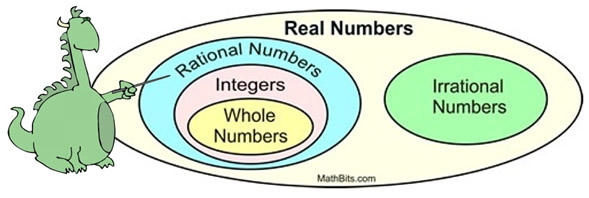
The rational numbers are "part" of the set of Real Numbers, which cover the entire number line.
Yep, there are a lot of rational numbers!
But there are even more Real numbers!
Between any two real (or rational) numbers, there is always another real (or rational) number.
FYI: The Real Numbers consist of all of the rational, as well as irrational, numbers.
So the Real number line below is "hiding" a lot of values between its hash marks!

 Arithmetic of Rational Numbers: Arithmetic of Rational Numbers:
Since you know how to add, subtract, multiply and divide fractions, you can apply these numeric arithmetic skills to rational numbers. We will take a quick review of these "numeric" fraction skills.
For those of you who want to know "why" things happen, we will also take a look "conceptually" and "graphically" as to what happens to the "signs" of rational numbers during arithmetic.
Numeric
MULTIPLY: |
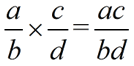 |
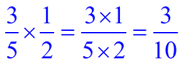 |
Multiply the tops and Multiply the bottoms.
Conceptually: Mathematics is consistent. If we know a rule, such as
"a number added to its opposite equals 0", or the "distributive property", we know these rules will remain true in all situations where they apply. We will use this consistency to establish how to determine the "signs" when multiplying signed numbers.
From our work with the natural numbers, we know that a "positive number times a positive number is a positive number".
Justifying Signs When Multiplying:
Situation 1:
positive number x negative number:
What is the answer to 4 x -5?
We know that 4(5 + -5) = 0
since 5 + -5 = 0.
Remember a number + its opposite = 0.
Now,apply the Distribute Property:
4(5 + -5) = (4 x 5) + (4 x -5) = 0
20 + (4 x -5) = 0
(4 x -5) must = -20.
Again, a number + its opposite = 0.
20 + -20 = 0
So, (4 x -5) = -20
Conclusion: A positive number x a negative number = a negative number.
The same process can be used to show that a negative number x a positive number = a negative number. |
Situation 2:
negative number x negative number:
What is the answer to -3 x -4?
We know that -3(4 + -4) = 0
since 4 + -4 = 0.
Remember a number + its opposite = 0.
Now,apply the Distributive Property:
-3(4 + -4) = (-3 x 4) + (-3 x -4) = 0
We discovered (on the left) that a positive number x a negative number = a negative number.
So (-3 x 4) = -12
Which gives us, -12 + (-3 x -4) = 0
(-3 x -4) must = +12.
Again, a number + its opposite = 0.
-12 + 12 = 0
So, (-3 x -4) = 12
Conclusion: A negative number x a negative number = a positive number. |
positive number x positive number = positive number (+) x (+) = (+)
negative number x negative number = positive number (-) x (-) = (+)
positive number x negative number = negative number (+) x (-) = (-)
negative number x positive number = negative number (-) x (+) = (-) |
(Hint: For multiply: when the signs are the same, the answer is positive. When the signs are different, the answer is negative.)

Numeric
DIVIDE: |
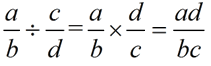 |
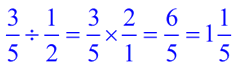 |
Flip the second number and follow the rules for multiplying.
Conceptually: Consider 4 ÷ -5. We learned from working with fractions that a division problem can become a multiplication problem by utilizing the reciprocal of the divisor.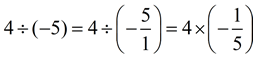
So, since we now have a multiplication problem, the rules that we generated for dealing with the "signs" when multiplying will also now apply to division. From our work with the natural numbers, we know that a "positive number divided by a positive number is a positive number".
positive number x positive number = positive number (+) x (+) = (+)
negative number x negative number = positive number (-) x (-) = (+)
positive number x negative number = negative number (+) x (-) = (-)
negative number x positive number = negative number (-) x (+) = (-) |
(Hint: When the signs are the same, the answer is positive. When the signs are different, the answer is negative.)

Numeric
ADD: |
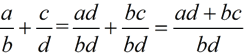 |
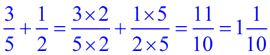 |
Get a common denominator. Then add the tops and keep the bottom.
Graphically: When adding rational numbers, p + q is the number located a distance | q | from p in the positive or negative direction depending upon whether q is positive or negative.
Situation: Adding a Positive:
p = -3 and q = 5 under Addition
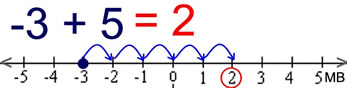 Start at -3. Adding +5 moves 5 units to the right.
Start at -3. Adding +5 moves 5 units to the right.
The movement is to the right because q = 5 is positive.
Answer = 2. |
Situation: Adding a Negative:
p = 1 and q = -3 under Addition
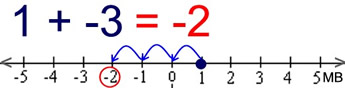 Start at 1. Adding -3 moves 3 units to the left.
Start at 1. Adding -3 moves 3 units to the left.
The movement is to the left because q = -3 is negative. Answer = -2. |

Numeric
SUBTRACT: |
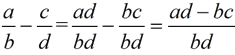 |
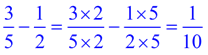 |
Get a common denominator. Then subtract the tops and keep the bottom.
Graphically: The subtracting of rational numbers can be thought of as adding the additive inverse,
p - q = p + (-q), which turns the problem into an addition problem. Follow the
procedure stated above for addition.
Situation: Subtracting a Positive:
(is adding a negative)
p = 2, q = 4, -q = -4 under Subtraction
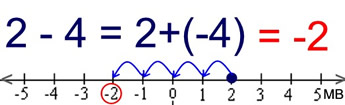 Start at 2. Adding -4 moves 4 units to the left.
Start at 2. Adding -4 moves 4 units to the left.
The movement is to the left since q = -4 is negative.
Answer = -2. |
Situation: Subtracting a Negative:
(is adding a positive)
p = 1, q = -3, -q = +3 under Subtraction
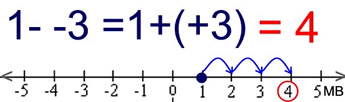 Start at 1. Adding +3 moves 3 units to the right.
Start at 1. Adding +3 moves 3 units to the right.
The movement is to the right since q = +3
Answer = 4. |
|