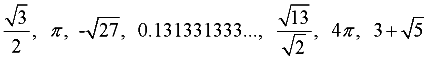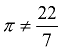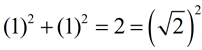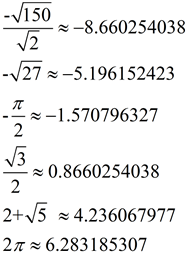|
Irrational numbers are numbers that cannot be written as the ratio of two integers. This means that they cannot be written as a fraction with an integer in the top and an integer in the bottom.
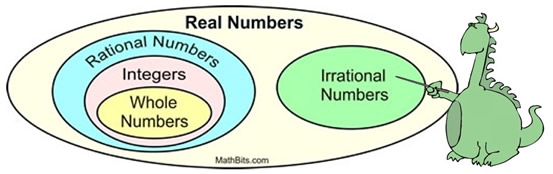
The Real Numbers are divided into two large subsets called " Rational Numbers" and " Irrational Numbers".
"Irrational" means not rational.
|
|
 |
An irrational number is a number that is NOT rational. It cannot be expressed as a fraction with integer values in the numerator and denominator. |
|
Examples: 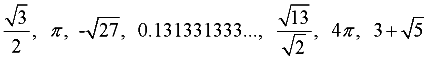
 When an irrational number is expressed in decimal form, When an irrational number is expressed in decimal form,
it goes on forever without repeating.
 Since irrational numbers are a subset of the real numbers, Since irrational numbers are a subset of the real numbers,
they possess all of the properties assigned to the real number system.
|
While it is popular to use 3.14 or 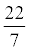 to represent "pi", these values are only estimates or approximations. Notice the differences in the decimal representations on the calculator screen at the right. |
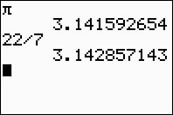 |
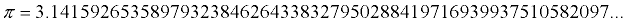 Pi (π) is an irrational number. Its decimal value goes on forever, and does not repeat.
Pi (π) is an irrational number. Its decimal value goes on forever, and does not repeat. |
|
 There are certain radical values which fall into the irrational number category. There are certain radical values which fall into the irrational number category.
 The square root of a non-perfect square is an irrational number. |
The square roots of perfect square numbers are integers and are rational numbers.
All other square roots, at this level, are irrational numbers.
For example, 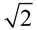 is irrational and cannot be written as a "simple fraction"
is irrational and cannot be written as a "simple fraction"
which has integers in the numerator and the denominator.
As a decimal,
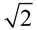 = 1.414213562373095048801688624 ... = 1.414213562373095048801688624 ...
which is a non-ending and non-repeating decimal, making 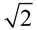 irrational. irrational.
The Pythagoreans thought this idea of drawing a length that could never be precisely measured was absurd, crazy, not reasonable, not rational, thus the name "irrational". Such numbers were thought to be imperfections of mathematics and their existence was hidden by the Pythagoreans. In fact, it is rumored that the Pythagorean (Hippassus), who first discovered this possibility, may have been thrown overboard during a sea voyage due to his discovery.

Irrational Numbers on a Number Line
By definition, a number line is a straight line diagram
on which every point
corresponds to a real number. |
 |
Since irrational numbers are a subset of the real numbers, and real numbers can be represented on a number line, one might assume that each irrational number has a "specific" location on the number line.
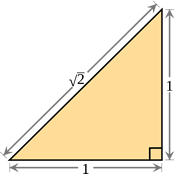
NOPE! The best we can do to locate irrational numbers on a number line is to "estimate" their locations. This is the same "measurement" problem we saw demonstrated in the right triangle above. You cannot measure a value that, as a decimal, is non-ending. And, you cannot locate the "exact" position of a non-ending decimal value on a number line.
|
"Estimates" of the locations of irrational numbers on number line:

So, what do the numbers shown on the number line above actually look like (as decimal values)?
Shown at the right are calculator estimates (approximations) of these irrational numbers.
Remember that these irrational numbers, when expressed as decimals, will be non-ending and non-repeating decimal values.
We cannot list their "exact" decimal values since they are non-ending decimals.
|
|
See Estimating Square Roots for clues on "how" to find out where
irrational numbers reside on the number line without a calculator.
|