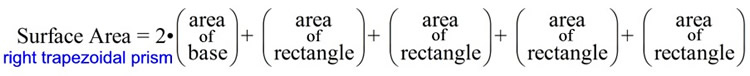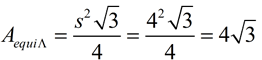For discussion on
using nets with surface area, see
Surface Area with Nets.
(Includes: right rectangular prism,
right triangular prism, right rectangular pyramid)
|
Surface area is the total area that the surface of a three-dimensional object occupies, in square units. |
|
Remember: Surface area is labeled in "
square units".
This lesson will be investigating the surface area of
right prisms and
right pyramids
composed of
triangles and
trapezoids.
 Right Prisms composed of triangles and trapezoids: |
|
• Right Triangular Prisms |
|
Use of the net is optional unless otherwise stated.
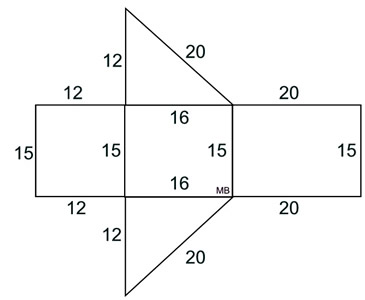
1. Find the surface area
of this right triangular prism.
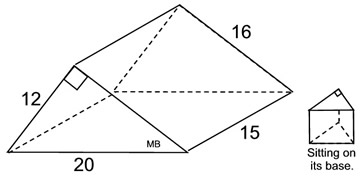
NOTE: The word "right" in this problem pertains to the status of the pyramid (not the triangle). "Right" in this context means the prism is such that if it sits on its base, its second base will be directly above the first base, It is just coincidence that the triangle used in this problem is also a "right" triangle.
What we know about this solid:
1. There are 5 faces.
2. There are 2 congruent right triangles (bases) with legs of 12 and 16.
3. There are 3 rectangular lateral faces.
4. The needed formulas:
rectangles: A = bh
triangles: A = ½ bh |
Using the net:
• Area of base right triangles: AΔ = ½ bh
=
½(12)(16) = 96 (2 of these)
• Area of 3 rectangles:
A1 = (12)(15) = 180
A2 = (16)(15) = 240
A3 = (20)(15) = 300 |
The surface area of this right triangular prism is the sum of the areas of all 5 faces.
Surface Area = 96 + 96 + 180 + 240 + 300 = 912 square units |
The work that was done in the example above can be combined to reveal
a "formula" for the surface area of a right prism.
B = area of the base
SA = 96 + 96 + 12•15 + 16•15 + 20•15
(now, factor 96 out of the first two areas, and factor 15 out of the last three areas)
= 2(96) + (12 + 16 + 20)•15
= 2(B) + (base perimeter) • prism height
The surface area, SA, of a right prism can be found
using the formula:
SA = 2B + ph
B = area of base, p = perimeter of base, h = prism height |
Use of the net is optional unless otherwise stated.
A "net" approach refers to examining "each" face one at a time.
2. Find the surface area
of this right
triangular prism. .
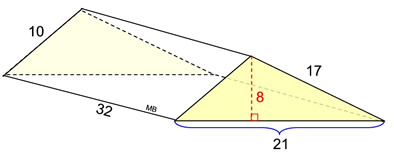
What we know about this solid:
1. There are 5 faces.
2. There are 2 congruent triangles (bases) shaded yellow.
3. There are 3 rectangular lateral faces.
4. Height of the triangle (base) is 8 units.
5. Height of the prism is 32 units.
6. The needed formulas:
rectangles: A = bh
triangles: A = ½ bh
Note these are scalene Δs (not right Δs) in this right triangular prism. |
Using net approach:
• Area of base triangles: AΔ = ½ bh =
½(8)(21) = 84 (2 of these)
• Area of 3 rectangles:
A1 = (10)(32) = 320
A2 = (17)(32) = 544
A3 = (21)(32) = 672
Surface Area = 84 + 84 + 320 + 544 + 672 = 1704 square units
Using the Formula: SA = 2B + ph
B = area of base Δ = 84
p = perimeter of Δ = 10 + 17 + 21 = 48
h = height of prism = 32
SA = 2B + ph
= 2(84) + 48(8) = 1704 square units |
• Right Trapezoidal Prisms: |
|
Yes, the formula stated in Example 1 (above) works for the Surface Area of ANY right prism,
and it will work for these right trapezoidal prisms.
The surface area, SA, of a right prism can be found
using the formula:
SA = 2B + ph
B = area of base, p = perimeter of base, h = prism height |
Use of the net is optional unless otherwise stated.
3. Find the surface area
of this right
trapezoidal prism.
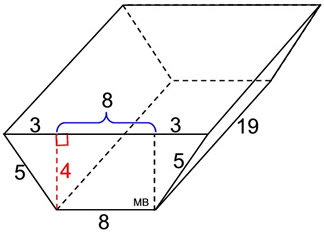
What we know about this solid:
1. There are 6 faces.
2. There are 2 congruent trapezoids (bases).
3. There are 4 rectangular lateral faces.
4. Height of trapezoid (base) is 4 units.
5. Height of the prism is 19 units.
6. The needed formulas:
rectangles: A = bh
trapezoid: A = ½ h (b1 + b2) or decompose |
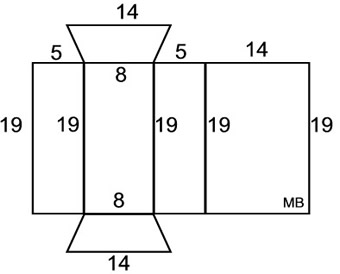
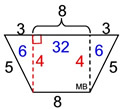
Using the net:
• Area of trapezoid bases:
A = ½ h ( b1 + b2) = ½ 4 (8 + 14)
= 44 square units (2 of these)
Or find the area of trapezoid by decomposing the figure into two triangles and a rectangle. Areas of the decomposed sections are in blue:
6 + 32 + 6 = 44 sq. units
(2 of these) |
 |
• Area of 4 rectangles:
A1 = (5)(19) = 95 A2 = (8)(19) = 152
A3 = (5)(19) = 95
A4 = (14)(19) = 266
|
The surface area of this right triangular prism is the sum of the areas of all 6 faces.
Surface Area = 44 + 44 + 95 + 152 + 95 + 266 = 696 square units
Using the Formula: SA = 2B + ph
B = area of base trapezoid = ½ h (b1 + b2) = ½ 4 (8 + 14) = 44
p = perimeter of trapezoid = 5 + 8 + 5 + 14 = 32
h = height of prism = 19
SA = 2B + ph
= 2(44) + 32(19) = 696 square units |
Use of the net is optional unless otherwise stated.
A "net" approach refers to examining "each" face one at a time.
| 4. Find the surface area
of this
right
trapezoidal prism.
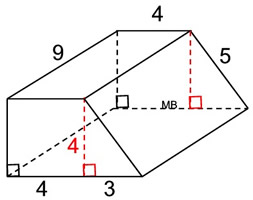
What we know about this solid:
1. There are 6 faces.
2. There are 2 congruent trapezoid (bases).
3. There are 4 rectangular lateral faces.
4. Height of trapezoid is 4 units.
5. The needed formulas:
rectangles: A = bh
trapezoids: A = ½ h (b1 + b2) or decompose |
Using net approach:
• Area of trapezoid bases:
Atrap = ½ h (b1 + b2) = ½(4)(4+7)
= 22 square units (2 of these)
Or find the area of trapezoid by decomposing the figure into a triangle and a rectangle. Areas of the decomposed sections are in blue:
6 + 1 6 = 22 sq. units (2 of these) |
 |
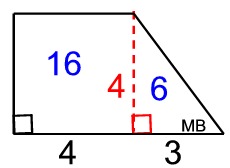• Area of 4 rectangles:
A1 = (4)(9) = 36
A2 = (5)(9) = 45
A3 = (7)(9) = 63
A4 = (4)(9) = 36
Surface Area = 22 + 22 + 36 + 45 + 63 + 36 = 224 square units
Using the Formula: SA = 2B + ph
B = area of base trapezoid = 22
p = perimeter of trapezoid = 4+7+5+4 = 20
h = height of prism = 9
SA = 2B + ph
= 2(22) + 20(9) = 224 square units
|
Right Pyramids composed of triangles and trapezoids: |
|
Working with pyramids can be a bit tricky.
Creating pyramids to meet our conditions (of being composed of triangles and trapezoids) is not as easy as it was when working with prisms. With a prism, basically either shape nicely created a right prism for which our formula applied (as well as the "net" method).
But with pyramids, there are conditions under which the formulas will apply, and situations where the formulas will NEVER apply leaving us only with a "net" method of solution.
Here is a quick summary of what you need to know about pyramids:
Regular Pyramids vs Irregular Pyramids
If the base of the pyramid is a regular polygon (with all sides equal, all angles equal), the pyramid is a regular pyramid. Otherwise, it is an irregular pyramid. |
Right Pyramids:
A pyramid being right means that the vertex (top point, apex) will be over the center of the base of the pyramid. The pyramid will "stand upright from its base"- it will not slant or lean over. ALL of our pyramids, at this level, are "right" pyramids. |
Formulas for Surface Area:
Right Pyramids with a regular polygon for the base can use a stated formula.
Right Pyramids not having a regular polygon for the base can NOT use a stated formula. |
Note: In certain problems, actual dimensions will be rounded for ease of calculation.
• Right Triangular Pyramids |
|
Use of the net is optional unless otherwise stated.
5. Find the surface area
of this
right regular triangular pyramid. Round answer to nearest hundredth of a square unit.
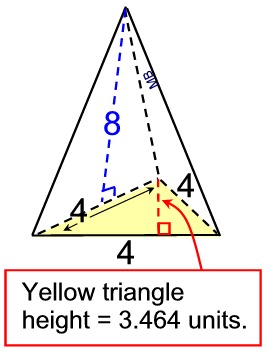
NOTE: The word "right" in this problem pertains to the status of the pyramid (not the triangle). "Right" in this context means the height of the pyramid goes from the vertex perpendicular to the base intersecting at the center of the base. It does not mean that the triangle is a right triangle.
What we know about this solid:
1. There are 4 faces.
2. There is one equilateral base triangle.
3. There are 3 congruent lateral face isosceles triangles each with a slant height of 8.
4. The needed formula: triangles
(A = ½ bh) or
special formula for equilateral triangle.
Note: Actual dimensions have been rounded to nearest thousandth.
|
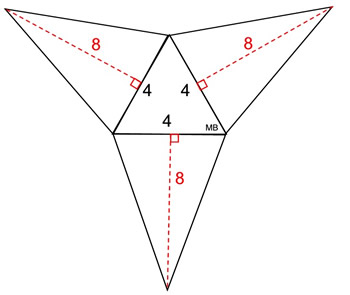
Using the net:
• Area of base equilateral triangle:
ABase Δ = ½(b)(h) = ½(4)(3.464) = 6.928
• Area of 3 congruent lateral triangles:
Alateral Δ = ½(4)(8) = 16 (3 of these)
Surface area = 6.928 + 16 + 16 + 16
= 54.928 = 54.93 square units
NOTE: If the equilateral triangle base had listed the lengths of the sides of the triangle only (not its height), you can find the area of the triangle by using a special formula just for equilateral triangles.(see statement of formula in box below)
The area of the yellow equilateral triangle: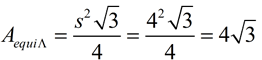 
which on a calculator gives 6.928. |
When working with a regular triangular base, you are working with a equilateral triangle. If you are only given the side lengths of the triangle, you may need a formula to find the area of that triangle:
s = side length |
Area (equilateral triangle)
|
|
|
Is there a surface area formula for pyramids like the one we saw for prisms?
The answer is "Yes", but it is not as applicable. Be careful!!!!
This surface area formula for pyramids is
ONLY for right "regular" pyramids.
The base MUST be a regular polygon (all sides equal, all angles equal)
in order to get a correct answer from this formula.
The surface area, SA, of a right "regular" pyramid
can be found
using the formula:
SA = B + ½ ph
B = area of base, p = perimeter of base, h = slant height |
Remember: The "slant height" is the height of one of the lateral faces
(not the height of the pyramid, which is perpendicular to the base).
Using this formula for Example 5 (above):
SA = B + ½ ph
B (from previous calculation = 6.928 )
SA = B + ½
ph = 6.928 + ½
(4 + 4 + 4)(8) =
54.93 square units
Right Trapezoidal Pyramids |
|
Trapezoids are NOT regular polygons.
No surface area FORMULA. |
A "net" approach will be needed in this problem. Examine "each" face one at a time.
6. Find the surface area
of this
right trapezoidal pyramid.
A trapezoid is not a regular polygon, so there will be no formula for this surface area of this pyramid. We will need to take the "net" approach and examine each face separately.
Information on the trapezoid base: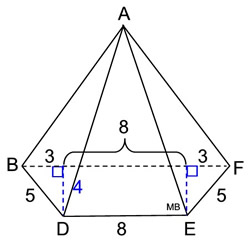
Information on the slant heights of the lateral faces. The slant height from point A to  is 12.2 units and the slant height from point A to  is 12.1 units.
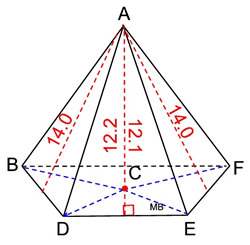
Since the trapezoid base is not a regular polygon, the slant heights in this pyramid will not all be the same length.
Note: Actual dimensions have been rounded to nearest tenth. |
What we know about this solid:
1. There are 5 faces.
2. There is one non-regular trapezoidal base.
3. The height of the trapezoid is 4 units.
4. There are 4 lateral faces which are triangles. Since this an isosceles trapezoid (legs equal), the areas of the left and right lateral faces will be the same. The front and back lateral faces do not have the same lateral height, nor the same area.
5. The needed formulas:
triangles: A = ½ bh
trapezoid:
A = ½ h (b1 + b2) (or decompose)
Using the net approach:
• First, let's examine the base and determine its area.
Area of trapezoid:
A = ½ h (b1 + b2) = ½ 4 (8 + 14) = 44
Or find the area of trapezoid by decomposing the figure into two triangles and a rectangle. Areas of the decomposed sections are in blue:
6 + 32 + 6 = 44 sq. units
|
|
• Area of 4 lateral triangles:
Alateral Δ = ½(b)(h)
A1 = ½(8)(12.2) = 48.8
A2 = ½(5)(14.0) = 35
A3 = ½(14)(12.1) = 84.7
A4 = ½(5)(14.0) = 35
Surface Area = 44 + 48.8 + 35 + 84.7 + 35
= 247.5 square units |
In the examples on this page, most of the measurements are integer values to allow for the emphasis to be placed on the process and easy computations. Now, that we have the idea of how these processes work, be on the look out for the return of more fractional, decimal, and radical measurements. Don't panic!! You can do this!
