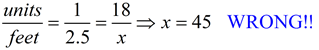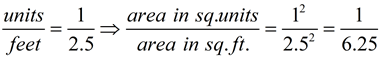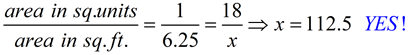logo

In this lesson, we will be examining scale drawings and areas,
when working on a grid or in a coordinate axes.

Working on a Dot Grid:

When a scale drawing is placed on a grid, be sure to
find out what each section on the dot grid represents.
Dot grids are primarily used with a scale representing square units (area),
but they may also be used to represent single units (length).
Notice how the different scale descriptions affects this problem.

This trapezoid is a scale drawing of a new sign to be placed in a store window.
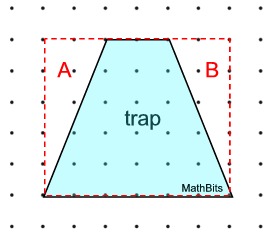  square unit= 2 square inchesgraphbluedottrap
What is the area of the actual sign?
Solution: We cannot count the squares.
• compose into a rectangle (box it in)
• subtract triangles' areas from box area
• adjust for 1 square = 2 square inches
Atrap = Abox - AΔA - AΔB

Atrap = 30 - 5 - 5 = 20 unit squares

Since 1 unit square = 2 square inches,
Atrap = 40 square inches.

This trapezoid is a scale drawing of a new sign to be placed in a store window.
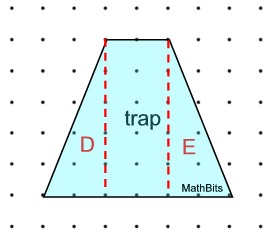unitone  = 2 inchesgraphbluedottrap
What is the area of the actual sign?
Solution: We are looking at segments.
• decompose into a rectangle and 2 Δs
• add areas of triangles and rectangle
• adjust for 1 length = 2 inches
Atrap = Arectangle + AΔD + AΔE

Atrap = 10 + 5 + 5 = 20 square units

Since 1 segment = 2 inches,
Atrap = 40 + 20 + 20 = 80 sq. inches

divider
Working on a Coordinate Grid:

Most coordinate grid questions dealing with area utilize the scales indicated on the x-axis and y-axis. When, however, the question is dealing with a scale drawing, you will need to look for a key as to how the scale drawing is related to the actual figure. When finding the area of figures whose sides do not lie on the lines of the grid, remember to use the "box" method.
Let's take a look at these options.

The triangle represents part of a billboard drawing.
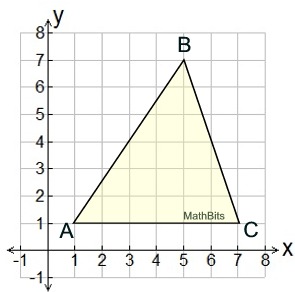
one unit length, key, = 1 footscalepic2
 What is the area of the actual shape?
AΔ = ½ bh
This is an easy problem. Count the base and the height to that base.
Scale ratio is easy at 1 unit to 1 foot.
A = ½ 6 • 6
Area = 18 square feet
The triangle represents part of a billboard drawing.
one unit length, key, = 2.5 footscalepic2
What is the area of the actual shape?
In this problem the scale ratio is
1 unit to 2.5 feet. Convert lengths:
Base 6 units = 15 feet.
Height 6 units = 15 feet.
A = ½ 15 • 15
Area = 112.5 square feet


QUESTION: In the second example shown above (on the right), would the area be the same answer if the unit area from the example on the left (18 square units) was simply multiplied by 2.5 to adjust for the scale? NO!

The area, in unit values from the grid,
is 18 square units.
If multiplied by 2.5, the area would be 45.
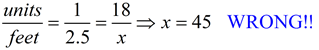
wrong
The area is 112.5 square feet.

frown

When working with scale drawings, you are working with similar figures.
One figure is simply an enlargement of the other.
In the lesson on similar figures, we discovered that:
• When dealing with lengths: In similar figures, the ratio of the corresponding sides, heights, diagonals, and perimeters are all the same ratio.
yellowblast • But when dealing with Area: In similar figures, the ratio of the areas is the SQUARE of the ratio of the corresponding sides.

Area is not a "measurement of length", so the ratio must be adjusted by squaring.
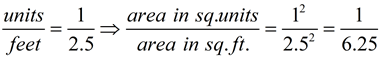
ratioareas

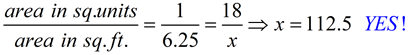
ratioYes
The area is 112.5 square feet.

frown

So, you can first convert the lengths (the sides) using the scale,
and then find the area.
Or, you can first find the unit area (from the graph),
and then convert using the square of the given scale ratio.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Use".