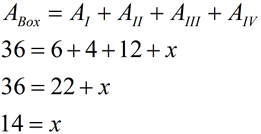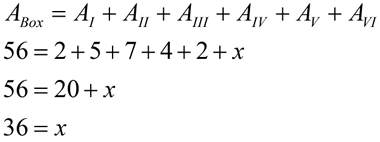logo

Finding the area of a polygon drawn on a coordinate axis can be an easy process, by either COUNTING or by using the simple BOX Method. Whether the "box" is needed, depends upon the placement of the polygon on the coordinate grid. Two situations are possible:
Sides are parallel to the axes:
If the polygon is drawn such that its sides (or needed segments) lie ON the grids of the graph paper, COUNT the lengths and use the appropriate area formula.
Sides are NOT parallel to the axes:
If the polygon is drawn such that its sides (or needed segments) do NOT lie ON the grids of the graph paper, draw the smalled possible "BOX" around the polygon to determine the area.
The "box" method is named for the process of "boxing in" (trapping) the shape inside of a rectangle so it cannot move.
The word "box", in this context, is not referring to a three-dimensional shape, called a "box" (like a cardboard box).

Sides are parallel to the axes:


COUNT to find the needed lengths.
The base of the triangle lies ON the grids of the graph paper (horizontal), and the height (vertical) also lies ON the grids of the graph paper, since a triangle's height is perpendicular to its base.

By counting, the base length is 7 units and the height is 3 units.
Use the area of a triangle formula:
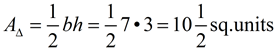
boxmath1
The answer is 10½ square units.

AC can also be found by subtracting the x-coordinates of the two points [4 - (-3) = 7]. Since the base of the height is located at (2,1), the height can be found by subtracting the y-coordinates [4 - 1 = 3].


box1
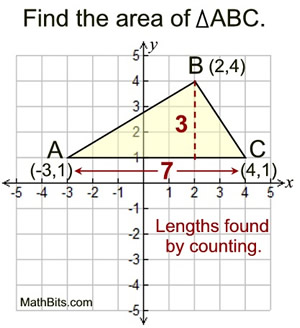
To COUNT: stand at A and take one step
to the right to the next grid line. Continue
stepping and counting until you reach C.
divider
Sides are NOT parallel to the axes:



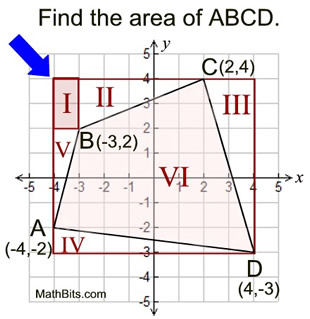
The sides of this ΔABC do NOT lie on the grid lines of the graph paper. Use the "Box Method" to solve for the area of the triangle.

• Draw the smallest "box" possible to enclose the polygon (ΔABC). Be sure that the "box" follows the grids of the graph paper.

• Number each of the parts of the box with a Roman numeral (ignore the axes when numbering).

• "The whole is equal to the sum of its parts." The area of each of the parts of the "box" added together equals the area of the "box".
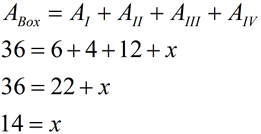boxarea2
The answer is 14 square units.

box2
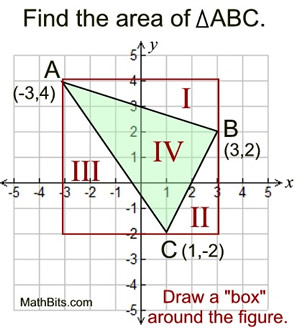The areas of the three right triangles
surrounding the figure are easy to find.
(count their bases and heights)
Note:
* Find the area of the box by counting.
* Represent the triangle you need by x.
* Find the area of each of the right triangles by counting and using the formula for the area of a triangle, ½bh.

This "Box" Method can also be referred to as
"composing into rectangles".

divider

Dealing with odd shaped pieces:


There may be times when the "box" will not form nice right triangles in each of the corners, as shown here in the upper left corner. In such a case, it is necessary to further subdivide this corner section into one rectangle and two right triangles, so the lengths can be easily counted.
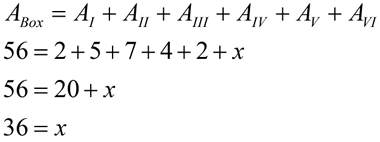
boxmath2
The answer is 36 square units.

box3a
Remember to keep your work simple by always forming shapes around the figure that are easy to count.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Use".