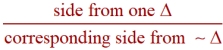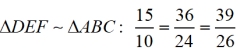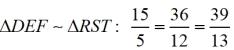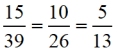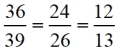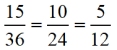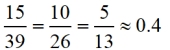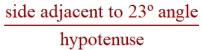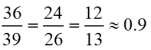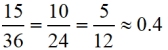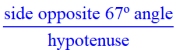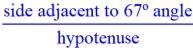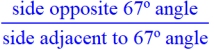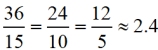|
In similar triangles, we know that the corresponding angles are congruent, and that the corresponding sides are in proportion. The corresponding sides are actually represented by ratios. These ratios then form proportions that allow for finding the lengths of missing sides.
On this page, the discussion starts with "ratios" in similar right triangles.

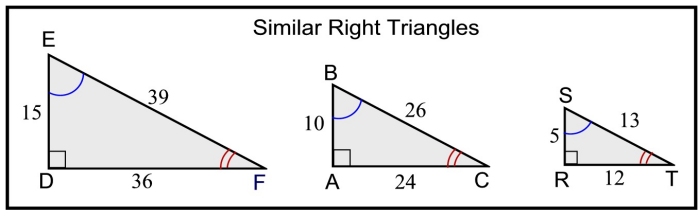
All three triangles, shown above, are similar right triangles. Notice the congruent angles.
There are several options when representing the ratios in similar triangles.
(Keep in mind that proportions can be rewritten in various forms yet remain true.)
Ratios formed
"between" Δs:
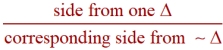
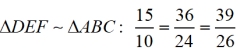
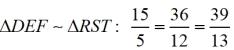
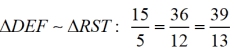
|
Ratios formed
"within" Δs:
(locations of sides remain "corresponding" between triangles) 
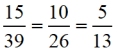
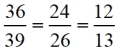
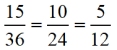
|

The equality of the corresponding ratios in similar triangles, of different sizes,
led Greek mathematicians to recognize a connection between
angles in triangles and the lengths of the sides of the triangles.
In this unit, the focus will be on ratios formed "within" Δs.
Specifically "within" right triangles, and their connection to the acute angles.
Let's add in some angle measures, and take another look these three similar right triangles.
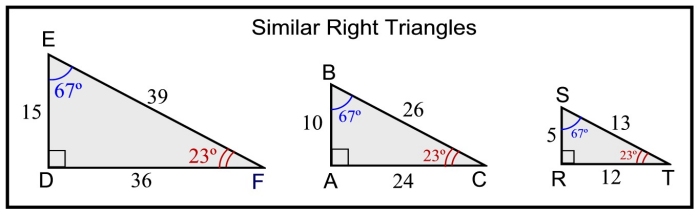
(Rounding to nearest integer has occurred.)
Ratios formed "within" Δs:
In relation to the 23º angle:

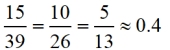
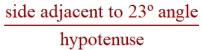
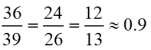

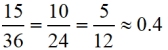
|
In relation to the 67º angle:
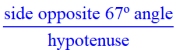
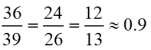
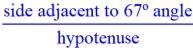
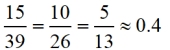
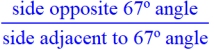
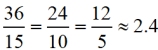
|
Things to notice about the chart above:
• Three specific ratio patterns are displayed.
• Each pattern's value is the same across all 3 Δs, dealing with 23º.
•
Each pattern's value is the same across all 3 Δs, dealing with 67º. |

"So, what?"
 |
We just saw that for EVERY right triangle contatining a 23º angle, these three ratio patterns will ALWAYS give the same answers.
If we change the degree of the angle, the values will differ, but will still ALWAYS give the same ratios for ALL right triangles containing that angle. |
|
Remember: All right triangles that have an acute angle measure in common, will be similar.
 In ALL right triangles containing an xº acute angle, In ALL right triangles containing an xº acute angle,
the values of each of these three ratio patterns
will be the same across all "sizes" of these similar triangles.
|
Remember: All right triangles that have an acute angle measure in common, are similar.
The equality of the ratios depends only on the size of the angles.
This discovery led to the establishment of a branch of mathematics
called "trigonometry" (meaning "triangle measure").
The 3 pattern ratios we have been examining are called "trigonometric ratios"
and will be further examined in the next lesson.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|