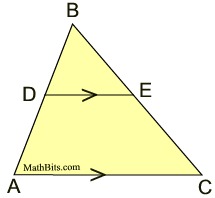
When working with similar figures, we will be working with a comparison of lengths in the form of ratios and proportions. Let's refresh what we know about ratios and proportions before we move on to similarity.
|
A ratio is a comparison of two (or more) quantities.
|
The ratio of one number to another number is a fraction.
It is the quotient of the first number divided by the second number,
where the second number is not zero. |
|
While a ratio is most commonly written as a typical fraction, (numerator over denominator),
it may also appear in other forms:
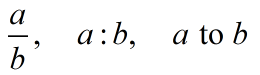
Since a ratio can be written as a fraction, it can also be written in any form that is equivalent to that fraction. All of the following statements are equivalent:
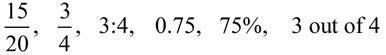
Equivalent ratios are ratios that can be reduced to the same value: 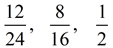
A continued ratio refers to the comparison of more than two quantities: a : b : c.
When working with ratios in an algebraic setting, remember that 3 : 4 : 7
may need to be expressed as 3x : 4x : 7x (an equivalent form).

The sides of a pentagon are in the ratio of 2 : 3 : 5 : 1 : 4. If the perimeter of the pentagon is 90 units, find the lengths of the five sides.
Solution: Represent the sides of the pentagon as 2x, 3x, 5x, x, and 4x, an equivalent form.
Since 2 + 3 + 5 + 1 + 4 does not equal 90, we know that the side lengths must be considered as an equivalent form of this continued ratio.
2x + 3x + 5x + x + 4x = 90
15x = 90
x = 6
The sides of the pentagon are 12, 18, 30, 6 and 24 units.

In dealing with similar triangles, we will be concentrating on proportions.
You will encounter the terms "proportion", "proportionality" and "proportionally".
|
A proportion is an equation stating that two ratios are equivalent (equal), written in the form 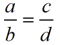 . |
|
Proportions always have an equal sign!
A proportion can be written in two forms: 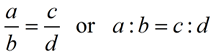
For example, 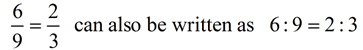
where both are read "6 is to 9 as 2 is to 3".
| Proportion:
|
In a proportion, the numbers a, b, c, and d are called the
first, second, third and fourth terms of the proportion respectively.
The first and fourth terms (6 and 3) are called the extremes.
The second and third terms (9 and 2) are called the means. |
Proportion:
|
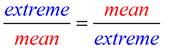 or
or 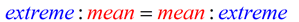
When written in the form extreme : mean = mean : extreme,
we can see that the "middle or inner" terms are the "means"
and the "outer terms" are the "extremes".
It is important to remember the terms "mean" and "extreme" in relation to a proportion.
We will encounter rules and theorems that reference these terms.
For example, consider the following "rule" that you learned about proportions.
 RULE: In a proportion, the product of the means RULE: In a proportion, the product of the means
equals the product of the extremes.
(You may see this rule referred to as "cross multiply" or "cross product".) |
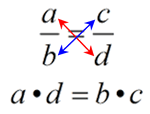 |

Properties of Proportions:
You will need to keep in mind that proportions can be written in different combinations, but still yield the same "cross product".

Notice that all of these proportions "cross multiply" to yield the same result.
a • d = c • b
 Keep in mind that there are many different ways to express
Keep in mind that there are many different ways to express
equivalent proportions (as shown above).
FYI: Other interesting properties about proportions:
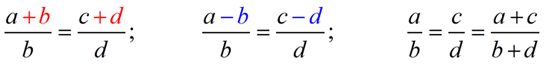


Using the RULE in numerical problems.
Solve for x: 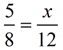
Solution: Apply the rule that "In a proportion, the product of the means equals the product of the extremes."
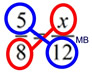 gives (5)•(12) = 8 • x; 60 = 8x; x = 7.5 ANSWER
gives (5)•(12) = 8 • x; 60 = 8x; x = 7.5 ANSWER

Using the RULE in geometric proofs.
In Geometry, we will also be using this rule when working with similar triangle proofs.


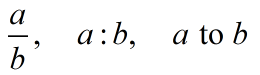
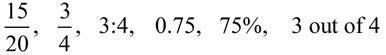
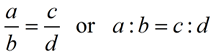
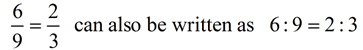
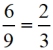
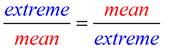 or
or 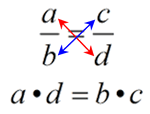

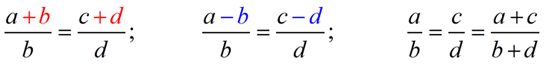
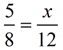
 gives (
gives (