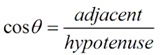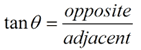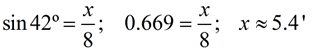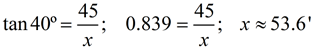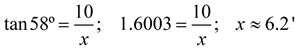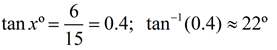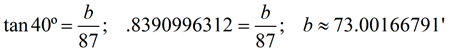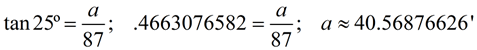|
Trigonometry's connection to measurement places it in the learner's manuals for a wide variety of professions. Carpenters, construction workers, designers, architects, and engineers, to name a few, deal with measurements, and as such, they deal with triangle measures, or trigonometry.
Combining your skills with similar triangles, trigonometry and the Pythagorean Theorem, you are ready to tackle problems that are connected to more real world scenarios. The situations you will be examining will be specifically related to right triangles, and you will be using our three main trigonometric functions.
Once a diagram is established, the mathematical solution will be the same as those shown on Solving for Sides or Solving for Angles.

There are two new vocabulary terms that may appear in application problems.
Angle of Elevation: |
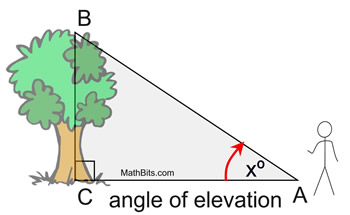
In this diagram, xº marks the
angle of elevation of the top of the tree
as seen from a point on the ground. |
The angle of elevation is always measured from the ground up. It is an upward angle from a horizontal line. It is always inside the triangle.
You can think of the angle of elevation in relation to the movement of your eyes. You are looking straight ahead and you must raise (elevate) your eyes to see the top of a tree.
When trying to remember the meaning of an angle of elevation think of an elevator that only goes up!
|
 |
|
Angle of Depression: |

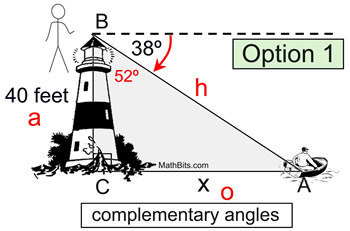
In this diagram, xº marks the
angle of depression of the boat at sea
from the top of the lighthouse. |
The angle of depression is always OUTSIDE the triangle. It is never inside the triangle. It is a downward angle from a horizontal line.
You can think of the angle of depression in relation to the movement of your eyes. You are standing at the top of the lighthouse and you are looking straight ahead. You must lower (depress) your eyes to see the boat in the water.
|
Notice how the horizontal line in the angle of depression diagram is PARALLEL to the ground level. The fact that horizontal lines are always parallel guarantees that the alternate interior angles are equal in measure. In the diagram, the angle marked xº is equal in measure to
m∠BAC. Simply stated, this means that ...
→ the angle of elevation = the angle of depression ← |
 |
When solving a problem with an angle of depression you need to find the measure of an angle INSIDE the triangle. There are two options:
Option 1: find the angle inside the triangle that is adjacent (next door) to the angle of depression. This adjacent angle will always be the complement of the angle of depression, since the horizontal line and the vertical line are perpendicular (90º). In the diagram at the left, the adjacent angle is 52º.
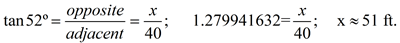 |
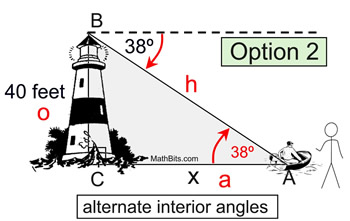 |
Option 2: utilize the fact that the angle of depression = the angle of elevation and label ∠BAC as 38º inside the triangle.
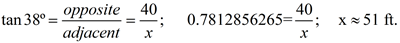
Notice that both options, the answer is the same.
|

Let's see how to put these skills to work in word problems.

A nursery plants a new tree and attaches a guy wire to help support the tree while its roots take hold. An eight foot wire is attached to the tree and to a stake in the ground. From the stake in the ground the angle of elevation of the connection with the tree is 42º. Find to the nearest tenth of a foot, the height of the connection point on the tree.
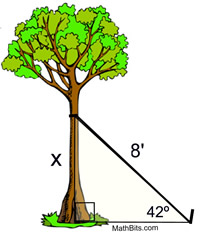 |
|
SOLUTION:
•
A "guy" wire is a support wire used to hold a newly planted tree in place, preventing it from bending or up-rooting during high winds.
• The "angle of elevation" is from the ground up.
• It is assumed that the tree is vertical, making it perpendicular with the ground.
• This problem deals with "opposite" and "hypotenuse" making it a sine problem.
• 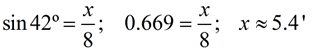
|

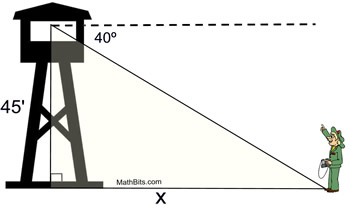
From the top of a fire tower, a forest ranger sees his partner on the ground at an angle of depression of 40º. If the tower is 45 feet in height, how far is the partner from the base of the tower, to the nearest tenth of a foot?
 |
|
SOLUTION:
•
Remember that the "angle of depression" is from a horizontal line of sight downward.
• It is assumed that the tower is vertical, making it perpendicular with the ground.
• This solution will use alternate interior angles from the parallel horizontal lines, so place 40º inside the triangle by the partner (bottom right).
• This solution deals with "opposite" and "adjacent" making it a tangent problem.
• 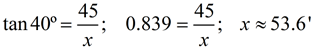
|

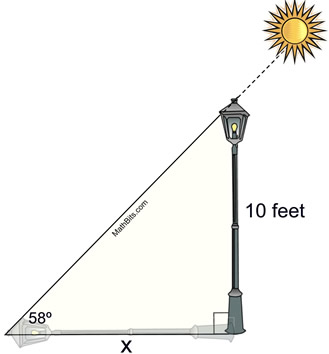
Find the shadow cast by a 10 foot lamp post when the angle of elevation of the sun is 58º. Find the length to the nearest tenth of a foot.
 |
|
SOLUTION:
•
Remember that the "angle of elevation" is from the horizontal ground line upward.
• It is assumed that the lamp post is vertical, making it perpendicular with the ground.
• Shadows are on the ground! If you place the "shadow" on the hypotenuse you have created an apparition ( a "ghost"), not a shadow!
• This solution deals with "opposite" and "adjacent" making it a tangent problem.
• 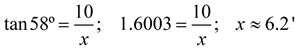
|

Not all trigonometry word problems will use the terms "angle of elevation" or "angle of depression". You may need to read carefully to see where to indicate the angle in the problem.
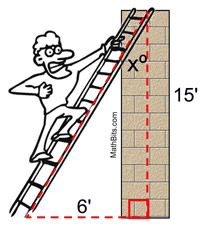
A ladder leans against a brick wall. The foot of the ladder is 6 feet from the wall. The ladder reaches a height of 15 feet on the wall. Find to the nearest degree, the angle the ladder makes with the wall.
 |
|
SOLUTION:
• In this problem place xº where the ladder meets the wall. Do not assume that the angle will always be at the ground level.
•
It is assumed that the wall is vertical, perpendicular with the ground.
• The foot of the ladder is the bottom of the ladder, where it hits the ground.
• This solution deals with "opposite" and "adjacent" making it a tangent problem.
• 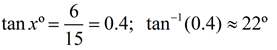
|

It may be the case that a problem will be composed of two overlapping right triangles.
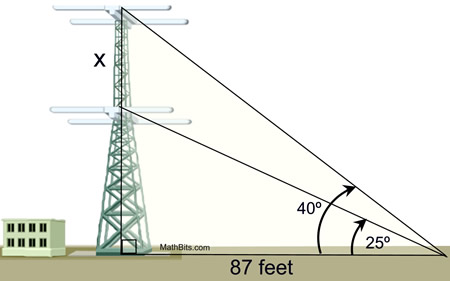
A radio station tower was built in two sections. From a point 87 feet from the base of the tower, the angle of elevation of the top of the first section is 25º, and the angle of elevation of the top of the second section is 40º. To the nearest foot, what is the height of the top section of the tower? |
 |
|
SOLUTION:
• Think of this problem as working with two separate triangles:
(1) the larger triangle with the 40º angle and a vertical side that represents the ENTIRE height, b, of the tower, and
(2) the smaller triangle with the 25º angle and a vertical side, a, that represents the height of the first (bottom) section of the tower.
• Solve for the vertical heights ( b and a) in the two separate triangles.
• The needed height, x, of the second (top) section of the tower will be the difference between the ENTIRE height, b, and the height of the first (bottom) section, a. You will need to subtract.
• In both triangles, the solution deals with "opposite" and "adjacent" making it a tangent problem.
• Larger triangle with height b: 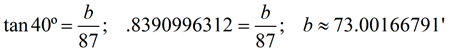
• Smaller triangle with height a: 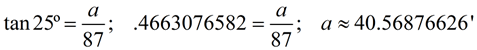
• Difference ( b - a): 73.00166791 - 40.56876626 = 32.43290165 ≈ 32 feet
 Notice, in this problem, that the trigonometric functions could not work directly on the side labeled "x" because that side was NOT the side of a right triangle. Notice, in this problem, that the trigonometric functions could not work directly on the side labeled "x" because that side was NOT the side of a right triangle.
|

Remember to set your graphing calculator to
DEGREE MODE. |
|
For help with
trig ratios on
your calculator,
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|