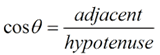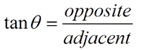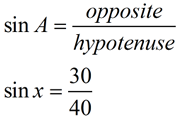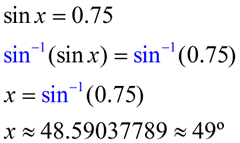|
Remember the three trigonometric functions that we will be using.
See Trigonometric Ratios for more information on labeling triangles and establishing these ratios.
One of the beauties of these trigonometric functions is that you can find the measure of an acute angle of a right triangle if you know two of the sides of the triangle.
 Using Trigonometric Functions to Find a Missing Angle |
The initial set up for solving these problems will be the same as that for finding a missing side.
To finish the problem, however, it will be necessary to use a calculator function referred to as an "inverse function" to find the actual number of degrees in the angle.
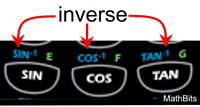
The inverse functions, on the graphing calculator, for each of the three trigonometric functions are found directly above the buttons for sine, cosine and tangent. They appear as sin-1, cos-1 and tan-1.
Note: sin-1(x) is read "the angle whose sine is x".
|
 |
You will discover, in later courses, that there are actually many angles whose sine is x, but in this course, we are looking for the simplest, most basic angle that has a sine x.
|
You can think of the inverse functions as "undoing" the trigonometric functions, leaving us with just the angle. 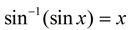 As your study of trigonometric inverse functions continues, you will see that sin-1(x), cos-1(x) and tan-1(x) may also be written as arcsin(x), arccos(x), and arctan(x), which are read "the arc whose sine is x", and so on.
Set Up the Diagram: |
Set Up the Formula: |
Find x, to the nearest degree.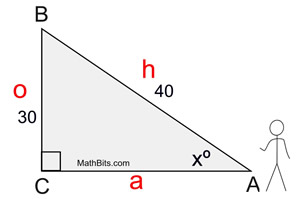 
Notice that in this problem, the x is INSIDE the triangle representing the angle. The a is alone, so this problem deals with o and h, which is sine. |
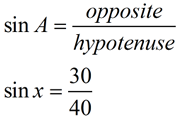
Now, divide 30 by 40 to change the fraction to a decimal.
sin x = 0.75
The goal now is to find an angle whose sine is 0.75. To do this, use the sin-1 function on your calculator!
|
On the graphing calculator: activate sin-1 (above the sin key) and then enter 0.75.
On the scientific calculator: enter 0.75 and then activate the sin-1 above the sin key.
Be sure you are in DEGREE MODE.
 |
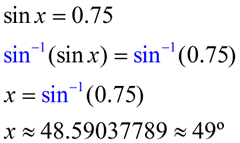These steps may also be written as:
|
|
ANSWER: x ≈ 49º |
When first learning about trigonometric ratios, you will be working in degree mode. Since the calculator defaults to Radian mode, be sure to
set your graphing calculator to
DEGREE MODE.
Also, use the full calculator entry when working a problem. Only round when you are ready for your final rounded answer.
|
|
For help with
trig ratios on
your calculator,
click here. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
