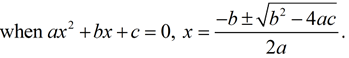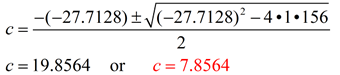|
We have seen combinations of sides and angles associated with the criteria for congruent triangles.
|
SAS - Side, Angle, Side
ASA - Angle, Side, Angle
AAS - Angle, Angle, Side
SSS - Side, Side, Side
HL - Hypotenuse Leg for Right Δs |
We saw that SSA (Side, Side, Angle) did not work to prove triangles congruent.
We politely called it the "Donkey Theorem." |
|
These combinations are now going to show us when to use the Law of Sines and Law of Cosines.
And yes, SSA is still going to be a trouble maker!
Using Law of Cosines with SSA |
We have seen that using the Law of Cosines with the combinations SAS and SSS guarantees one unique solution and one unique triangle. Working with the third option of SSA, however, continues to leave the door open for several different situations to occur, as it did with the Law of Sines. SSA is still referred to as the Ambiguous Case.
Unlike the Ambiguous Case for the Law of Sines, the Ambiguous Case associated with the Law of Cosines will always require the solution to a quadratic equation to find a missing side.
Dig out the old quadratic formula: 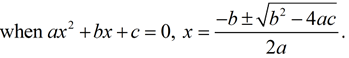
SSA: If two sides and the non-included angle are given, three situations may occur.
When dealing with the Law of Cosines, you will be looking to find a side.
| |
(1) NO triangle exists - no solution
(2) TWO different triangles exist - 2 solutions
(3) exactly ONE triangle exists - 1 solution. |
|
|
|
SSA - Two sides and the non-included angle are given.
|
Situation 1: NO triangle exists. |
In ΔABC, m∠A = 30º, a = 7, and b = 16.
Find c.
Solution:

|
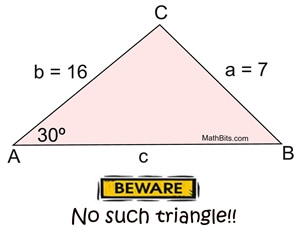
ANSWER: This triangle does not exist. |
The solution shows that this triangle does not exist because there is no real number solution to the quadratic equation. We need real number values to represent the sides of a triangle. |
|
SSA - Two sides and the non-included angle are given.
|
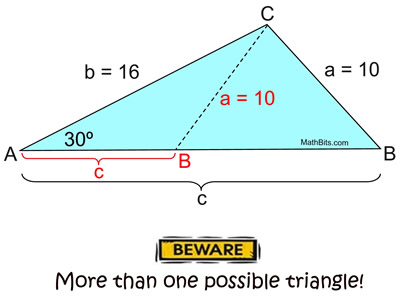
Situation 2: TWO triangles exist. |
In ΔABC, m∠A = 30º, a = 10, and b = 16.
Find c.
Solution:
Since angle A is the only known angle, choose the Law of Cosines formula that utilizes angle A.
 Now, use the quadratic formula to solve for c.
Now, use the quadratic formula to solve for c.
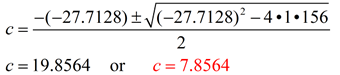
|
ANSWER: c = 19.8564
or c = 7.8564
There are two possible triangles.
|
The quadratic equation solution shows that there are two possible solutions for c, which means there are two possible triangles (one acute triangle and one obtuse triangle). |
|
SSA - Two sides and the non-included angle are given.
|
Situation 3: Exactly ONE triangle exists. |
In ΔABC, m∠A = 30º, a = 20, and c = 16.
Find c.
Solution:
 |
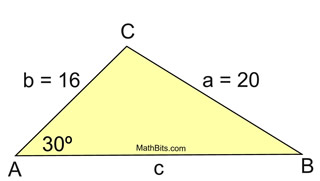
ANSWER: c = 32.1866979
ONE distinct triangle exists. |
| There is only one possible solution. Since c represents the side of a triangle, it must be a positive value. The negative solution is rejected. |

To summarize the Ambiguous Case:
Unlike the Ambiguous Case for the Law of Sines with all of its possible situations, the Ambiguous Case for the Law of Cosines leaves the decision making on the number of triangles (or solutions) to the quadratic equation.
The solution(s) to the quadratic equation tell you the needed information:
(1) if the solution is "not Real", the triangle does not exist (no solution).
(2) if the solution is "two Real positive values", there are two possible triangles (2 solutions).
(3) if the solution is "one positive and one negative Real values", there is one triangle (1 solution).

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|