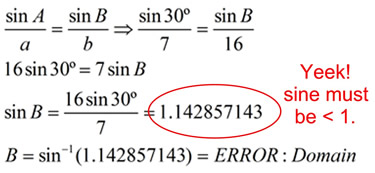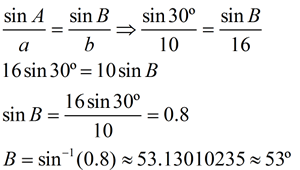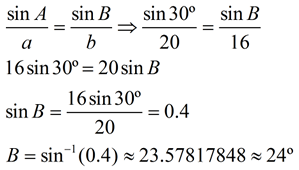|
We have seen combinations of sides and angles associated with the criteria for congruent triangles.
|
SAS - Side, Angle, Side
ASA - Angle, Side, Angle
AAS - Angle, Angle, Side
SSS - Side, Side, Side
HL - Hypotenuse Leg for Right Δs |
We saw that SSA (Side, Side, Angle) did not work to prove triangles congruent.
We politely called it the "Donkey Theorem." |
|
These combinations are now going to show us when to use the Law of Sines and Law of Cosines.
And yes, SSA is still going to be a trouble maker!
Using Law of Sines with SSA |
We have seen that using the Law of Sines with the combinations ASA and AAS guarantees one unique solution and one unique triangle. Working with the third option of SSA, however, leaves the door open for several different situations and solutions to occur. For this reason, SSA is referred to as the Ambiguous Case.
|
Ambiguous means open to two or more interpretations. |
|
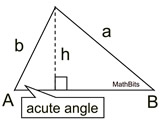
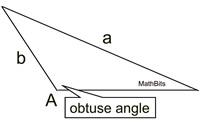
SSA: If two sides and the non-included angle are given, three situations may occur.
When dealing with the Law of Sines, you will be looking to find an angle.
| |
(1) NO triangle exists - no solution
(2) TWO different triangles exist - 2 solutions
(3) exactly ONE triangle exists - 1 solution |
|
|
 FACTS to remember about Law of Sines and SSA triangles: FACTS to remember about Law of Sines and SSA triangles:
1. In a triangle, the sum of the measures of the interior angles is 180º.
2. No triangle can have two obtuse angles.
3. The hypotenuse is always the longest side in a right triangle. So, when working in a triangle with 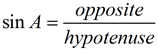 , sin A must be less that +1 (and greater than -1). , sin A must be less that +1 (and greater than -1).
4. The sine of an obtuse angle is defined to be the sine of its supplementary acute ∠. |
|
SSA - Two sides and the non-included angle are given.
|
Situation 1: NO triangle exists. |
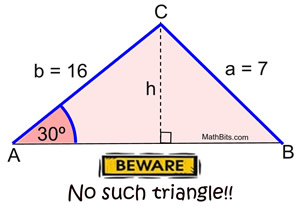
In ΔABC, m∠A = 30º, a = 7, and b = 16.
This question may ask "Find m∠B" or "How
many distinct triangles can be drawn with
these measurements?"
Solution: The Law of Sines will show that a triangle
with these conditions does not exist.
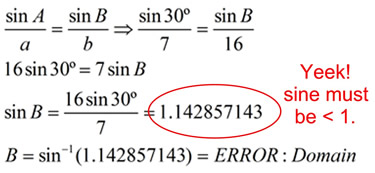
|
Since sin A = h/b, substitution gives h = 8. But, now we have a hypotenuse of 7 in a right triangle with a leg of 8. The hypotenuse is always the longest side in a right triangle. This diagram is not possible. |
ANSWER: m∠B cannot be found.
NO such triangle exists. |
| In relation to triangles, sin B must be < +1 for angle B to exist. No triangle exists in this problem. |
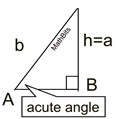
SSA - Situation 1:
No Triangle
Exists
 |
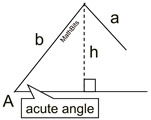 If A is acute and a < h,
If A is acute and a < h,
no triangle exists.
|
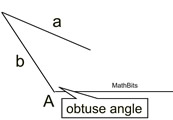 If A is obtuse and a
If A is obtuse and a  b, b,
no triangle exists. |
|
|
SSA - Two sides and the non-included angle are given.
|
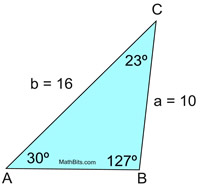
Situation 2: TWO different triangles exist. |
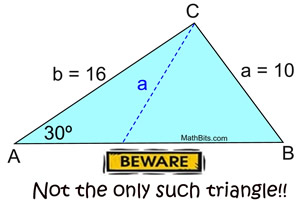
In ΔABC, m∠A = 30º, a = 10, and b = 16.
This question may ask "Find m∠B" or "How
many distinct triangles can be drawn with
these measurements?"
Solution:
Let's solve for measure of ∠B.
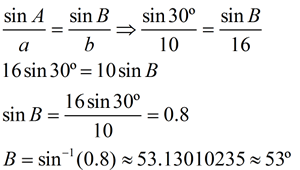
|
We can see right away that the problem that existed in Example 1 is not a problem with this triangle. The value of a is larger than the height from C (8) and a triangle will be formed. But, if we swing side a from point C to the left, can we form a second triangle? |
|
If m∠B = 53º and m∠A = 30º,
then m∠C = 97º. Looks good!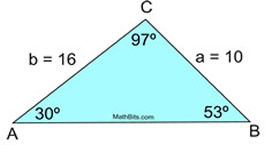 |
But wait! We know that the sine
of an obtuse angle is the sine of
its supplement. We must consider that
sin 53º is also sin 127º.
The triangle could be m∠B =127º,
m∠A = 30º, and m∠C = 23º.
ANSWER: m∠B = 53º OR 127º
TWO distinct triangles exist. |
|
|
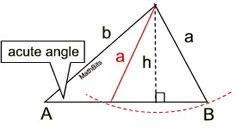
SSA - Situation 2:
TWO Δs Exist
 |
In this situation, h < a < b.
Since a is larger than h, a Δ is created. But since a is smaller than b, it can "swing" to the left of h and create a second triangle containing an obtuse angle.
|
|
|
|
SSA - Two sides and the non-included angle are given.
|
Situation 3: Exactly ONE triangle exists. |
In ΔABC, m∠A = 30º, a = 20, and c = 16.
This question may ask "Find m∠B" or "How
many distinct triangles can be drawn with
these measurements?"
Solution:
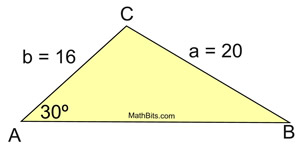
Since we have info about ∠A, go to the formula:
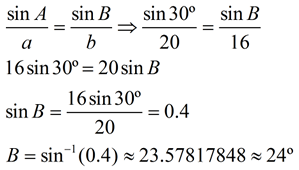 |
Note: The supplement of 24º is 156º, which is too large to be considered an angle in this triangle.
(156º + 30º is already > 180º) |
ANSWER: m∠B = 24º
ONE distinct triangle exists. |

To summarize the Ambiguous Case:
| When working with SSA, given m∠A, side a (opposite ∠A) and side b: (h = b sin A) |
Acute ∠A |
Acute ∠A |
Acute ∠A |
Acute ∠A |
Obtuse ∠A |
Obtuse ∠A |
a < h |
a = h |
a > b > h |
b > a > h |
a 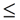 b b |
a > b |
no Δ |
one rt. Δ |
one Δ |
two Δs |
no Δ |
one Δ |
What to look for when dealing with Ambiguous Case:
When using the Law of Sines with SSA, consider the value of sine (-1 < sin B < +1) and the supplemental angle possibilities:
Outcomes: |
Look for: |
0 triangles |
sine value is out of range (remember -1 < sin B < +1) |
1 triangle |
supplementary angle does not fit in the triangle |
2 triangles |
supplementary angle fits in the triangle |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|


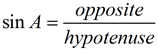 , sin A must be less that +1 (and greater than -1).
, sin A must be less that +1 (and greater than -1).