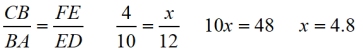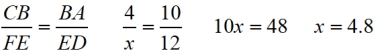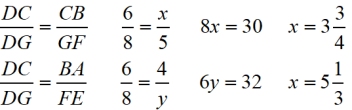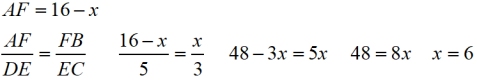We have seen that working with similarity means working with proportions.
In preparation for an upcoming theorem, let's take a look at a theorem that directly addresses a connection between "parallel lines" and "proportional line segments".
This theorem is called the "Proportional Line Segment Theorem", and will be
a precursor to the "Triangle Side Splitter Theorem"
(seen in the next lesson).

|
Proportional Line Segment Theorem: Three or more parallel lines intercept proportional segments on two or more transversals. |
|
Find x: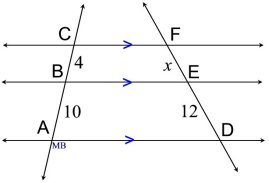 |
In this diagram, there are 3 parallel lines intersecting 2 transversals. The parallels are dividing the transversals proportionally.
Options as to how to represent the proportions.
• by ratios ON each line:
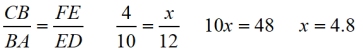
• by corresponding ratios ACROSS lines: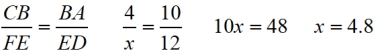
(This option will be in keeping with an upcoming theorem.) |

Find x and y: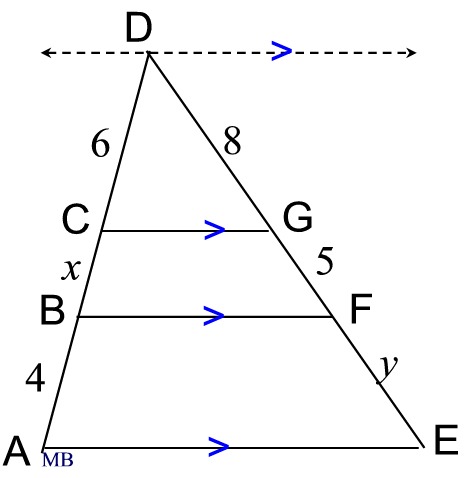 |
In this diagram, there are actually 4 parallel lines. One of the parallel lines passes through the point where the transversals (which are the sides of the triangle) intersect.
(Normally, you would not see the dashed line in the diagram.)
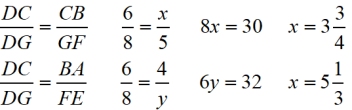
Notice how, when the transversals intersect, the problem becomes a triangle. |

Find x:
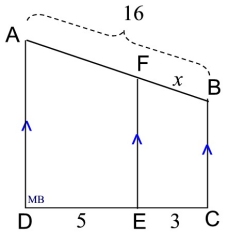 |
In this diagram, the parallel lines are vertical.
More algebra thinking is required in this problem.
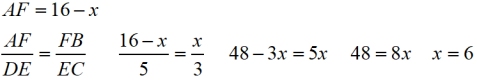
|