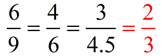|
Figures with the same shape, but not necessarily the same size,
are said to be "similar".
These cartoon dogs are exactly the same shape, but are not the same size.
The dog on the right is an enlargement
of the dog on the left.
While these dog figures are not congruent, they are similar. |
 |
|
 |
Polygons are similar if their corresponding angles are congruent (equal in measure) and the ratios of their corresponding sides are proportional. |
(This definition allows for congruent figures to also be "similar", where the ratio of the corresponding sides is 1:1.) |
While "similarity" applies to all polygons, we will be focusing on "similarity" as applied to triangles.
Facts about similar triangles: |

|
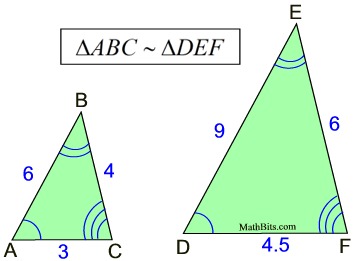
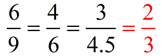
The ratio of the corresponding sides is called
the ratio of similitude or scale factor.
|
Similar Symbol:
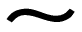
|
The symbol used to express "similar" was also seen in the symbol for "congruent" (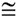 ). But unlike congruent, similar does not imply = size. ). But unlike congruent, similar does not imply = size. |
|
Similar figures are figures that are the same shape, but not necessarily the same size.
Similar figures can also be defined in relation to transformations:
 Transformations
Transformations |
Two figures are similar if and only if one figure can be obtained from the other by a single transformation , or a sequence of transformations, including translations, reflections, rotations and/or dilations. |
|
 A similarity transformation is a transformation in which the image has the same shape as the pre-image. A similarity transformation is a transformation in which the image has the same shape as the pre-image.
The study of rigid transformations (isometries) showed a connection between congruent figures and the transformations of types called translations, reflections, and rotations. Rigid transformations preserve size and shape.
|
Rigid Transformations
Translations
Reflections
Rotations
"same shape and same size"
(congruent) |
Similarity Transformations
Translations
Reflections
Rotations
Dilations
"same shape"
(similar) |
|
Similarity transformations include translations, reflections, and rotations, with the addition of dilations. Similarity transformations preserve shape, but not necessarily size, making the figures "similar".
Since it is possible for similar figures to have a scale factor of 1 (making the shapes the same size), it can be said that all congruent figures are also similar. Keep in mind, however, that most similar figures do not preserve size.
Are these triangles similar?
If it is possible to find one, or more,
transformations that will move one triangle
to coincide with the other,
the triangles will be similar.
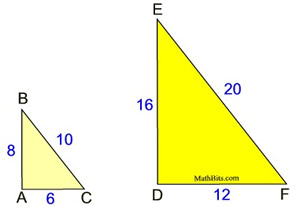 |
Yes, these triangles are similar.
If ΔABC is dilated by a scale factor of 2,
and then translated to the right and up,
it will coincide with ΔDEF.
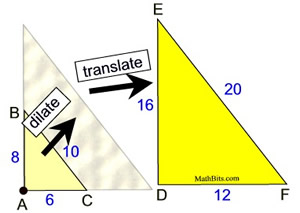 |
We could have guessed that these triangles would be similar since they are both right triangles (their sides satisfy the Pythagorean Theorem), and their sides are generated from the same Pythagorean Triple of 3,4,5 (6,8,10 and 12,16,20). But, now we can "prove" that they are similar since we found the similarity transformations that allow one triangle to coincide with the other.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|