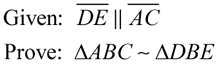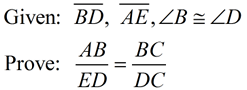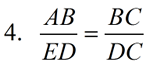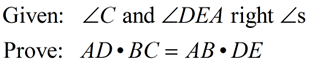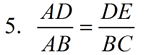The basic proof problems involving similar triangles will ask you to prove one of three things:

1. the triangles are similar,
2. a proportion is true, or
3. a product is true.

Of course, there are additional proof problems that utilize similar triangles to gather needed information about the triangles to prove an unrelated concept.

The examples below will demonstrate the three basic options
typically associated with similar triangle proofs.

When asked to prove triangles similar:

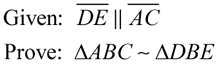
pf1pTG

Start by looking for 2 sets of congruent angles (AA), since AA is the most popular method for proving triangles similar.
(If AA is not working, your other options
are SSS or SAS for similar triangles.)
pfp1
Statements
Reasons
pfp11a
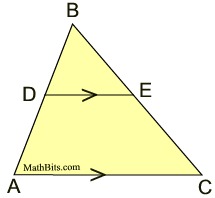
1. Given
2. ∠B 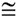congruent ∠B
Both triangles share ∠B.
2. Reflexive property
3. ∠BDE 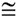congruent ∠A
3. If 2 || lines are cut by a transversal, the corresponding angles are congruent.
4. ΔABC ∼ ΔDBE
4. AA - if 2∠s of one Δ are 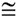congruent to the corresponding ∠s of another Δ, the Δs are similar.

 


When asked to prove a proportion to be true:

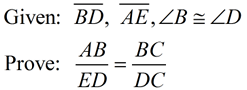
pfpr2G

Proportions are associated with similar triangles. Start by proving the triangles similar.
If working with multiple triangles, find the triangles whose
sides match the lengths in the proportion.

pfpr2a
Statements
Reasons
pfpr2T11
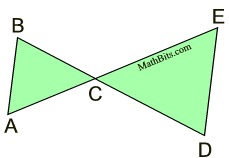
1. Given
2. ∠BCA 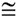congruent ∠DCE
2. Vertical angles are congruent.
3. ΔABC ∼ ΔEDC
3. AA - if 2∠s of one Δ are 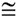congruent to the corresponding ∠s of another Δ, the Δs are similar.
pfpr2T4
4. The corresponding sides of similar triangles are proportional.

 

 

When asked to prove a product to be true:

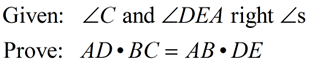
pfpr3T1

When you "cross multiply" a proportion, you will get a product. Prove the triangles are similar, then set up a proportion that will yield this product.
pfpr3
Statements
Reasons
pfpr3T2
1. Given
2. ∠C 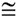congruent ∠DEA
2. All right angles are congruent.
3. ∠A 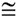congruent ∠A
3. Reflexive property.
4. ΔADE ∼ ΔABC
4. AA - if 2∠s of one Δ are 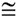congruent to the corresponding ∠s of another Δ, the Δs are similar.
pfpr3T5
5. The corresponding sides of similar triangles are proportional.
pfpr3T6
6. In a proportion, the product of the means equals the product of the extremes.

 


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".