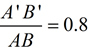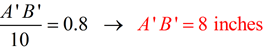|
Now that we have connected dilations to work in the coordinate plane, let's take a look at what happens to lines and line segments under a dilation.
We will be looking at three dilation concepts connected to lines and segments:
1. a line passing through the center of the dilation (result: the same line)
2. a line not passing through the center of dilation (result: parallel lines)
3. a line segment's length in a dilation (result: x scale factor) |

| Concept 1: A dilation leaves a line passing through the center of the dilation unchanged. It will remain the same line. |
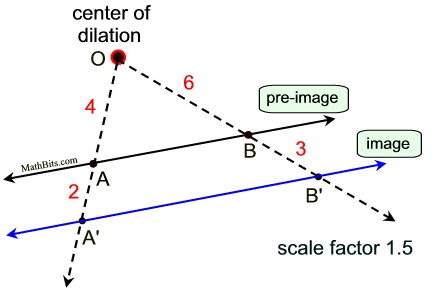
What happens if we dilate an entire line, with the center of dilation ON the line?
If that line passes through the point which is the center of the dilation, nothing will change.
| Remember that the image point formed by a dilation will lie on a straight line connecting the pre-image point to the center of the dilation. |
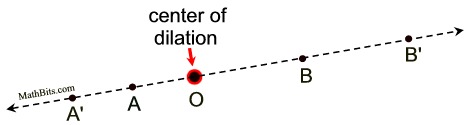 |
In this case, where the center of the dilation lies ON the given line being dilated, the "line connecting the pre-image to the center of the dilation" is the given line itself.
The diagram above shows 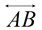 with a center of dilation, labeled O, located on the line. If we choose point B as our pre-image point, we know that its image after the dilation will lie on the line through O and B, which is, of course, with a center of dilation, labeled O, located on the line. If we choose point B as our pre-image point, we know that its image after the dilation will lie on the line through O and B, which is, of course, 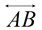 , the same given line. , the same given line.
Since O is located on 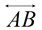 , the image of any point on , the image of any point on 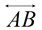 will lie on will lie on 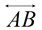 . .
| Conclusion: The dilation of the line, with the center of dilation on the line, leaves the line unchanged (we get the same line again). The scale factor is of no importance. |

| Concept 2: A dilation takes a line NOT passing through the center of the dilation to a parallel line. |
What happens if we dilate an entire line, but the center of the dilation in NOT on the line?
It is important to keep in mind that dilations also create parallel "segments" when dealing with figures.
 When a figure is dilated, a segment (side) of the pre-image that does not pass through the center of dilation will be parallel to its image. When a figure is dilated, a segment (side) of the pre-image that does not pass through the center of dilation will be parallel to its image.
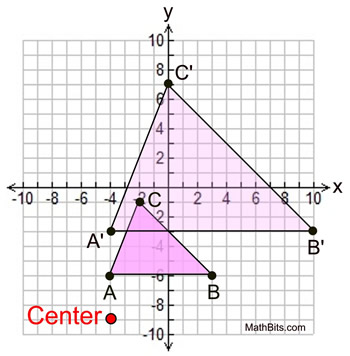
In the diagram at the right, with center of dilation at (-4,-9) and scale factor of 2, we have
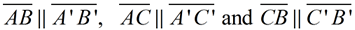 . . |
|
| Concept 3: The dilation of a line segment is longer or shorter in the ratio given by the dilation scale factor. |
If the scale factor is greater than 1 (k > 1), the image will be larger than the pre-image, making the segments (sides) of the image longer than the corresponding sides of its pre-image (an enlargement).
A'C' > AC; A'B' > AB; B'C' > BC
If the scale factor is 2, we will have
A'C' = 2AC; A'B' = 2AB; B'C' = 2BC
Also, notice that the pre-image will be between the center of dilation and the image.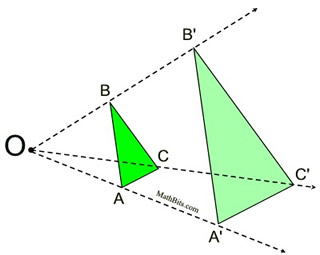
Note: If the absolute value of the scale factor is greater than 1, the image will be larger than the pre-image.
(When k < -1, the image is larger, with a 180º rotation.
The negative symbol indicates direction.) |
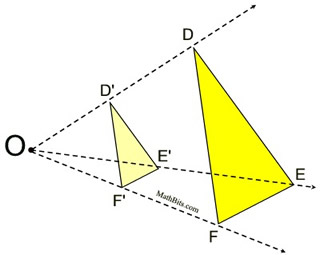
If the scale factor is between 0 and 1
(0 < k < 1), the image will be smaller than the pre-image, making the segments (sides) of the image smaller than the corresponding sides of its pre-image (a reduction).
D'E' < DE; D'F' < DF; F'E' < FE
If the scale factor is ½, we will have
D'E' = ½DE; D'F' = ½DF; F'E' = ½FE
Also notice that the image will be between the center of dilation and the pre-image.
 Note: If the absolute value of the scale factor is between 0 and 1, the image will be smaller than the pre-image.
Note: If the absolute value of the scale factor is between 0 and 1, the image will be smaller than the pre-image.
(When -1< k < 0, the image is smaller, with a 180º rotation. The negative symbol indicates direction.) |
If k = 1 (or k = -1), the image and pre-image are the same size (congruent). |

Given: 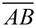 is 10 inches long. is 10 inches long.
If
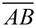 is dilated to form is dilated to form 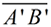 with a scale factor of 0.8, find the length of with a scale factor of 0.8, find the length of 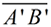 . .
Solution:
We know that the ratio of the length of the image to the length of the pre-image is equal to the scale factor.
Since we know 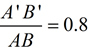 , we can substitute AB = 10, and solve for our answer. , we can substitute AB = 10, and solve for our answer.
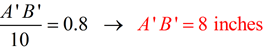

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


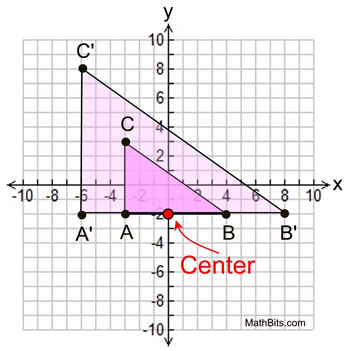
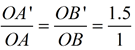 , where O-A-A' and
, where O-A-A' and