Let's restate what we already know about dilations and lines
to now emphasize the "equations" of the lines.

1. a line passing through the center of the dilation (result: the same line)
RE: Equations
• If the center of the dilation lies on the given line, then the original line and the dilation line lie on top of one another. The line is its own image.
• The given line and the dilated line will have the same linear equation.
• Both lines will have the same slope and the same y-intercept.

2. a line not passing through the center of dilation (result: parallel lines)
RE: Equations
• If the center of the dilation is not on the given line, then the dilation line will be parallel to the given line.
• The slopes of the two lines will be the same, since parallel lines have equal slopes.
• The y-intercepts of the two lines will not be the same.

NOTE:
• If the center of dilation is the origin, the y-intercept of the dilation line will be the
y-intercept of the given line, multiplied by the scale factor.

dividerdash

Concept 1: center of a dilation lies ON the given line ...
* The equations of the line and its dilation will be the same equation.
The scale factor is of no importance.

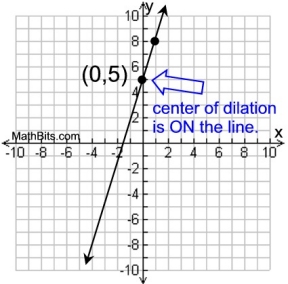
The line represented by the equation y = 3x + 5 is dilated by a scale factor of 3 centered at (0,5). What is the equation of the image of the line after the dilation?

The center of the dilation, (0,5), lies ON the line.

We know from our work with dilations, that when the center of the dilation lies on a line, all of the images of points on that line will also fall on that line.

The equation of the dilation will be the SAME as the equation of the given line, y = 3x + 5.

bulletANSWER: equation y = 3x + 5
\

dividerdash

 

Concept 2: center of a dilation does NOT lie on the given line ...
* The equations of the given line and its dilated line have the same slope,
but not the same y-intercepts.
 Multiply y-intercept by scale factor ONLY if dilation center is origin, (0,0).

The line represented by the equation y = 2x + 3 is dilated by a scale factor of 3 centered at the origin. What is the equation of the image of the line after the dilation?

The center of the dilation, (0,0), lies OFF the line.
This means the dilated line will be parallel to the given line, having the same slope but a different y-intercept.

The slope of the given line is m = 2.
The dilated line will have the same slope of 2.

The y-intercept of the given line is b = 3.
Since the center of dilation is the origin, the y-intercept can be found by multiplying the given line's y-intercept by the scale factor. (3 x 3 = 9)
The y-intercept of the dilated line is 9.

bulletANSWER: equation y = 2x + 9

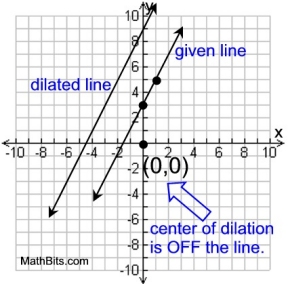
The distance from the origin to the y-intercept of the given line is 3 units along the y-axis. By the definition of a dilation, the image of this y-intercept point will be the distance along this same y-axis for 3 times the length, giving the dilated point to be 9 units from the origin along the y-axis.

dividerdash

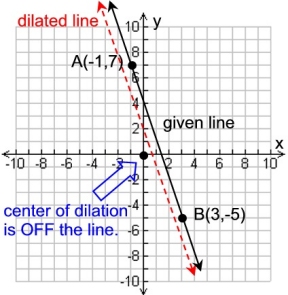
Given a straight line through points A(-1,7) and B(3,-5). The line is dilated by a scale factor of ½ centered at the origin. What is the equation of the image of the line after the dilation?

Write the equation of the line through the two points.
Compute the slope of the line (7-(-5))/(-1-3) = -3.
Using the slope, the y-intercept will be b = 4.
The equation of the given line is y = -3x + 4.

The center of the dilation, (0,0), lies OFF the line.
The dilated line will have the same slope of -3.
Since the dilation is at the origin, we know that the
y-intercept will be 4 x ½ = 2.

bulletANSWER: equation y = -3x + 2

 \

dividerdash
 

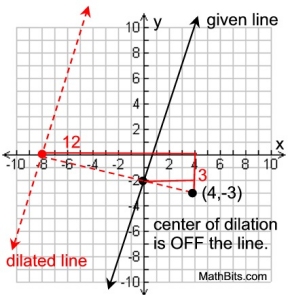
The line represented by the equation y = 3x - 2 is dilated by a scale factor of 3 centered at (4,-3).
Find the equation of the image of the line after the dilation?

Due to the location of the center of dilation (not the origin), this problem will require applying the concepts of a dilation, and a bit more work.

Establish a point on the dilated line using y-intercept
at (0,-2) on the given line :
• from the dilation center, (4,-3), move up one unit and 4 units left, arriving at the y-intercept of the given line. To find the coordinating dilated point, apply the scale factor to these lengths: start at (4,-3) and move up 3 units and left 12 units. Dilated point (-8,0).
("move up 1, left 4" becomes "move up 3, left 12" by scale factor of 3)


Write the equation of the dilated line using the point (-8,0):
The slope of the dilated line will be the same as the slope of the given line, which is 3.
y - y1 = m(x - x1)           y - 0 = 3(x - (-8))           y = 3x + 24     

bulletANSWER: equation y = 3x + 24


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".