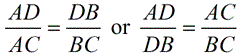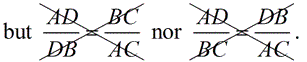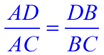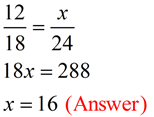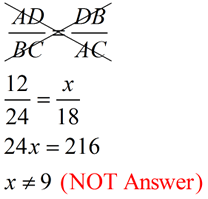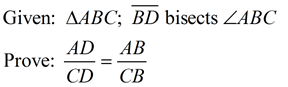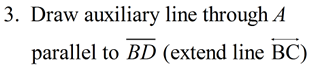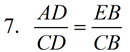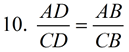|
The "Angle Bisector" Theorem says that an angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other two sides of the triangle.
 Be sure to set up the proportion correctly. While proportions can be Be sure to set up the proportion correctly. While proportions can be
re-written into various forms, be sure to start with a correct arrangement.
For example, in the diagram shown below, a correct proportion may be:
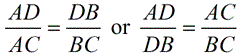 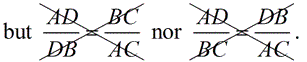 |
Find x.
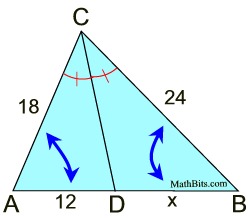 |
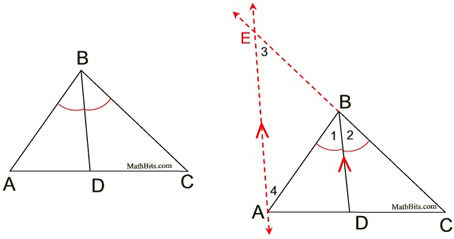
It may be helpful to remember that the segments formed by the angle bisector will form a correct proportion when paired with their adjacent triangle sides, such as:
|

|
An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle.
(proof below) |
|
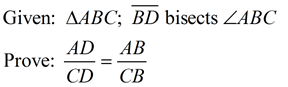
Auxiliary lines will be needed
to create similar triangles.
|
|
Proof:
Statements |
Reasons |
|
1. Given |
|
2. An angle bisector is a ray in the interior of an angle forming two congruent angles. |
|
3. Parallel Postulate: through a point not on a line there is only one line parallel to the given line. |
|
4. If 2 || lines are cut by a transversal, the corresponding angles are congruent. |
|
5. If 2 || lines are cut by a transversal, the alternate interior angles are congruent. |
|
6. Substitution |
|
7. Side Splitter Theorem: If a line is || to one side of a triangle and intersects the other 2 sides, it divides the sides proportionally. |
|
8. If 2 angles of a triangle are congruent, the sides opposite the angles are congruent (Isosceles triangle). |
|
9. Congruent segments have = lengths. |
|
10. Substitution |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|