|
You have worked with these angle concepts in past courses.
Let's refresh and enhance some basic facts about working with angles.
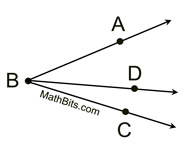
If D lies in the interior of ∠ABC, then
m∠ABD + m∠DBC = m∠ABC. |
This concept may also be referred to as
"whole quantity" or "the whole is equal to the sum of its parts." |
 |
|
An angle bisector is a ray from the vertex of the angle into the interior of the angle forming two congruent angles.
|
|
| |
|
|
Remember that the word "bisect" means to cut into two equal measured pieces.
m∠1 = m∠2 |
Note: You may see this definition say "two angles of equal measure", instead of "two congruent angles."
It depends on the textbook you are using.
| If a point lies anywhere on an angle bisector, that point is equidistant from the two sides (rays) of the bisected angle. |
Allow the shortest distance from D
to the rays
be determined by
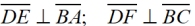
ΔBDE can be proven congruent to ΔBDF using:
• ∠1 congruent to ∠2
• the right ∠s congruent
(∠BED and ∠BFD)
• shared side from B to D
Triangles congruent by AAS.
By CPCTC, it can be shown that DE = EF (equidistant). |
Congruent triangles can show that DE = EF
m∠1 = m∠2
by the angle bisector |


Angles Forming a Straight Line |
If the non-shared sides of two, or more, adjacent angles form a straight line, the measures of the angles add up to 180º.
|
|
| |
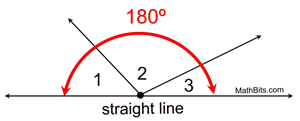
m∠1 + m∠2 + m∠3 = 180º
|
This is a "common sense" rule. A straight line is also a straight angle, which contains 180º. If these angles are adjacent (don't overlap), and their non-shared sides form a straight line, the angles comprise a straight angle which contains 180º. |
If two, or more, adjacent angles completely surround a point, the measures of the angles add up to 360º.
|
|
| |
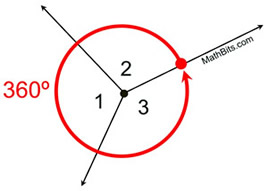
m∠1 + m∠2 + m∠3 = 360º
|
This is also a "common sense" rule. The complete revolution around a point is a circular 360º. If these angles are adjacent (don't overlap), and together they form one complete revolution, the measures of the angles will total 360º.
You might also think of this concept in a setting where you have two straight angles on either side of a straight line (which will also total 360º).
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|