|
When a transversal intersects two or more lines in the same plane, a series of angles are formed. Certain pairs of angles are given specific "names" based upon their locations in relation to the lines. These specific names may be used whether the lines are parallel or not parallel.
|
"Names" given to pairs of angles:
| |
• alternate interior angles |
| |
• alternate exterior angles |
| |
• corresponding angles |
| |
• interior angles on the same side of the transversal |
|
|

Let's examine these pairs of angles in relation to parallel lines:
Alternate Interior Angles:
The word "alternate" means "alternating sides" of the transversal.
This name clearly describes the "location" of these angles.
When the lines are parallel,
the measures are equal.
|
|
|
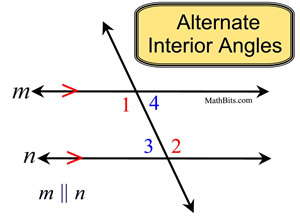
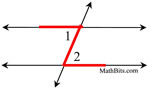
∠1 and ∠2 are alternate interior angles
∠3 and ∠4 are alternate interior angles |
Alternate interior angles are "interior" (between the parallel lines), and they "alternate" sides of the transversal. Notice that they are not adjacent angles (next to one another sharing a vertex).
When the lines are parallel,
the alternate interior angles
are equal in measure.
m∠1 = m∠2 and m∠3 = m∠4 |
|
If you draw a Z on the diagram, the alternate interior angles can be found in the corners of the Z. The Z may also be backward: 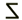 .
  |
|
|
If two parallel lines are cut by a transversal, the alternate interior angles are congruent. |
|
 Converse
Converse |
If two lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel. |
|

|
Alternate Exterior Angles:
The word "alternate" means "alternating sides" of the transversal.
The name clearly describes the "location" of these angles.
When the lines are parallel,
the measures are equal.
|
|
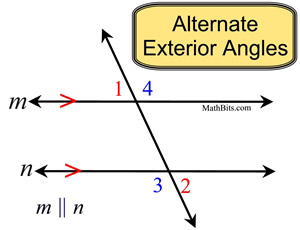
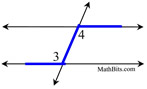
∠1 and ∠2 are alternate exterior angles
∠3 and ∠4 are alternate exterior angles |
Alternate exterior angles are "exterior" (outside the parallel lines), and they "alternate" sides of the transversal. Notice that, like the alternate interior angles, these angles are not adjacent.
When the lines are parallel,
the alternate exterior angles
are equal in measure.
m∠1 = m∠2 and m∠3 = m∠4 |
|
If two parallel lines are cut by a transversal, the alternate exterior angles are congruent. |
|
 Converse
Converse |
If two lines are cut by a transversal and the alternate exterior angles are congruent, the lines are parallel. |
|

Corresponding Angles:
The name does not clearly describe the "location" of these angles. The angles are on the SAME SIDE of the transversal, one INTERIOR and one EXTERIOR, but not adjacent.
The angles lie on the same side of the transversal in "corresponding" positions.
When the lines are parallel,
the measures are equal.
|
|
 |
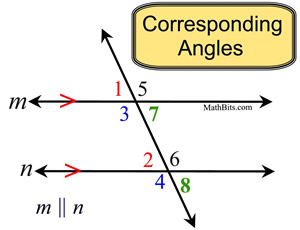
∠1 and ∠2 are corresponding angles
∠3 and ∠4 are corresponding angles
∠5 and ∠6 are corresponding angles
∠7 and ∠8 are corresponding angles |
If you copy one of the corresponding angles and you translate it along the transversal, it will coincide with the other corresponding angle. For example, slide ∠ 1 down the transversal and it will coincide with ∠2.
When the lines are parallel,
the corresponding angles
are equal in measure.
m∠1 = m∠2 and m∠3 = m∠4
m∠5 = m∠6 and m∠7 = m∠8 |
|
If you draw a F on the diagram, the corresponding angles can be found in the corners of the F. The F may also be backward and/or upside-down:  .
  |
|
|
If two parallel lines are cut by a transversal, the corresponding angles are congruent. |
|
 Converse
Converse |
If two lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel. |
|
FYI: These two corresponding angle theorems are in fact, "theorems". They are not postulates!
A "theorem"
is a statement that can be proven true.
A "postulate" is a statement assumed to be true, but cannot be proven true.

 |
Interior Angles on the Same Side of the Transversal:
The name is a description of the "location" of the these angles.
When the lines are parallel,
the measures are supplementary.
|
Also called "consecutive interior angles" or "same side interior angles". |
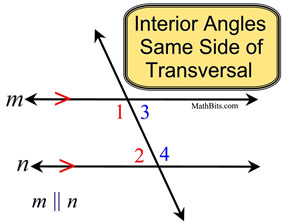
∠1 and ∠2 are interior angles on the same side of transversal
∠3 and ∠4 are interior angles on the same side of transversal |
These angles are located exactly as their name describes. They are "interior" (between the parallel lines), and they are on the same side of the transversal.
When the lines are parallel,
the interior angles on the same side of the transversal are supplementary.
m∠1 + m∠2 = 180
m∠3 + m∠4 = 180 |
|
If two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary. |
|
 Converse
Converse |
If two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary, the lines are parallel. |
|

In addition to the 4 pairs of named angles that are used when working with parallel lines (listed above), there are also some pairs of "old friends" that are also working in parallel lines.
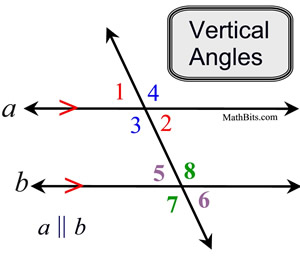
Vertical Angles:
When straight lines intersect, vertical angles appear.
Vertical angles are ALWAYS equal in measure,
whether the lines are parallel or not.
|
|
 |
|
There are 4 sets of vertical angles in this diagram!
∠1 and ∠2
∠3 and ∠4
∠5 and ∠6
∠7 and ∠8
Remember: the lines need not be parallel to have vertical angles of equal measure. |
|
Vertical angles are congruent. |
|

 |
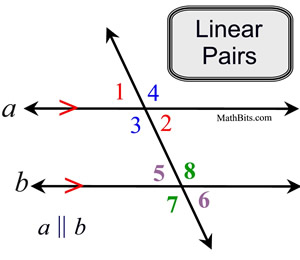
Linear Pair Angles:
A linear pair are two adjacent angles forming a straight line.
Angles forming a linear pair are
ALWAYS supplementary.
|
|
|
Since a straight angle contains 180º, the two angles forming a linear pair also contain 180º when their measures are added (making them supplementary).
m∠1 + m∠4 = 180
m∠1 + m∠3 = 180
m∠2 + m∠4 = 180
m∠2 + m∠3 = 180
m∠5 + m∠8 = 180
m∠5 + m∠7 = 180
m∠6 + m∠8 = 180
m∠6 + m∠7 = 180 |
|
If two angles form a linear pair, they are supplementary. |
|



NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|