 |
Remember -- use your compass
and straightedge only! |
|
Parallel - through a point |
|
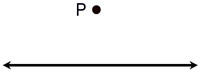
Given: point P not on a given line
Construct: a line through point P parallel to given line.
|
|
STEPS:
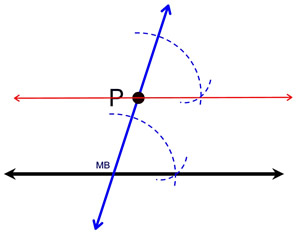
1. Using your straightedge, draw a transversal through point P. This is simply a straight line which passes through P and intersects with given line. Drawing the line slanted will make the construction easier than if you draw the line vertical. Be sure to draw the line well above P.
2. Using the construction COPY AN ANGLE, construct a copy of the angle formed by the transversal and the given line such that the copy will be located UP at point P. The vertex of the copied angle will be point P.
3. When you draw the line to complete the angle copy, you will be drawing a line parallel to the given line.
Alternate Method:
 |
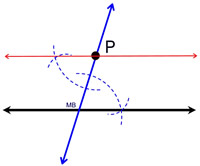
The construction above shows the creation of congruent corresponding angles which make the lines parallel. As shown at the right, you can also copy the angle below P and to its left, creating alternate interior angles and parallel lines.
The corresponding angle approach is often preferred because it prevents the construction lines for the angles from bumping into one another. |
 |

Proof of Construction: By using the COPY AN ANGLE construction, we created two angles of equal measure (which are also congruent). In relation to the parallel lines, these two angles are positioned in such a manner that they are called corresponding angles. A theorem regarding parallel lines tells us: If two lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel. (Change the words "corresponding angles" to "alternate interior angles" and you have the proof for the Alternate Method.)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|