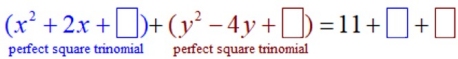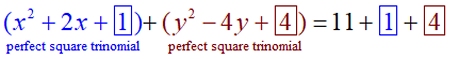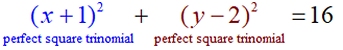Completing the Square for Circles (2 variables) MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

NOTE: Regarding "completing the square", the same testing limitations apply for NY NGMS Geo as applied to NY NGMS A1. Completing the square will involve leading coefficient is 1 (or a coefficient of 1 after removal of a greatest common factor), with an even linear term. This site will cover these expectations,.as well as additional information and concepts

The Algebra Refresher reminded us that the secret to completing the square is
the creation of a perfect square trinomial.

When working with one variable (x), our goal was to find one perfect square trinomial.
But, now that we will be working with two variables (x and y), our goal will be to find
two perfect square trinomials - one associated with each variable.

When we are working with circle equations, we will be working with x² and y².
In addition, the coefficients of these variables will be positive and of the same numeric value.

Let's take a look at how to work with two perfect square trinomials.

Example: Completing the Square with two variables:

1. Group all of the x terms together, and group all of the y terms together.	x2 + 2x + y2 - 4y - 11 = 0
2. If there is a constant term on the left side of the equation, move the constant term to the right side.	x2 + 2x + y2 - 4y = 11
Important: We are now going to work on EACH VARIALBE SEPARATELY: We will create a perfect square trinomial for EACH variable.
3. Set up the problem. Separate the variable and get ready to work on establishing a perfect square trinomial for each variable. Inserting boxes may remind you to add the values to BOTH sides of the equation.
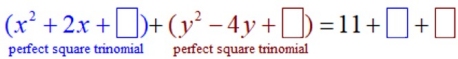4. Remember this strategy from Algebra: "take half of the coefficient of the middle (linear) term and square it. Add these values to both sides of the equation.
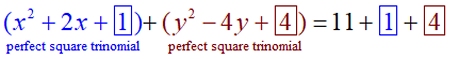5. Factor the perfect square trinomials.
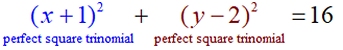This is the format we will be using when working with equations of circles. This circle has a center at (-1,2) and a radius of 4.

Example: Completing the Square with two variables and coefficients:

1. The coefficients of the squared variables are the same numeric values and are both positive, but they are not equal to 1. Divide through by 2.	x2 + y2 - 8x - 6y + 16 = 0
2. Group all of the x terms together, and group all of the y terms together.	x2 - 8x + y2 - 6y + 16 = 0
3. If there is a constant term on the left side of the equation, move the constant term to the right side.	x2- 8x + y2 - 6y = -16
Create a perfect square trinomial for EACH variable.
4. Set up the problem. Then "take half of the coefficient of the middle (linear) term and square it. Add these values to both sides of the equation.
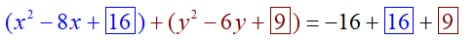5. Factor the perfect square trinomials.
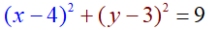This circle has a center at (4,3) and a radius of 3.