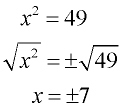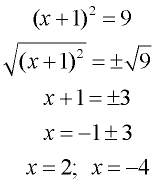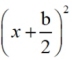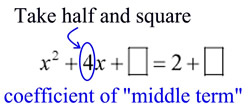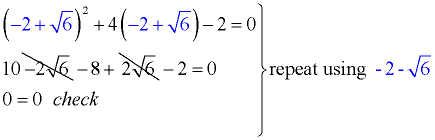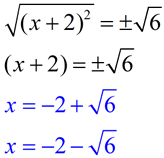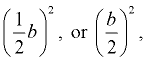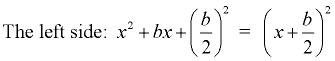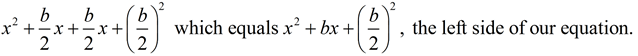|
 Completing the Square in ONE variable.
Completing the Square in ONE variable.
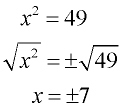
Perfect square
on the left side
(and right side in this problem) .
|
|
When solving an equation involving a perfect square (such as x2 = 49 seen at the left), taking the square root of both sides of the equation quickly yields the result.
This same square rooting process works nicely on equations with the square of a binomial on the left side (such as
(x + 1)2 = 9 as seen at the right). We could even replace
(x + 1)2 with x2 + 2x + 1, and start with a perfect square trinomial on the left side. |
|

|
Creating a perfect square trinomial on the left side of a quadratic equation, after moving the constant (number) to the right, is the basis of a process called completing the square.
|
In plain English, we are going to "force" a perfect square trinomial
on the left side
of the equation which will allow us to quickly solve a quadratic equation
by using the "square rooting method".
Before we talk more about the "process" of completing the square, let's take a look at how a perfect square trinomial is connected to its factored form (a binomial squared).
Quadratic trinomial: x2 + bx + c
Factored form: (x + p)2
Conclusion: (from work at the right)
b = 2p
c = p2
|
|
Factored form (a binomial squared):
(x + p)2
(x + p) • (x + p)
x2 + px + px + p2
x2 + 2px + p2
Perfect square trinomial:
 |
|
Example:
So, if we start with x2 + 8x,
we need to find a value for c to create
a perfect square trinomial.
We get x2 + 8x + 16. |
b, the coefficient of 8x, is 8 = 2p
p = 4
The c term will be p2 = 42 = 16 |
|
In plain English, to find c, we took half of the coefficient of b, and squared that value. 
So, how do we "force" a perfect square trinomial on the left side?
The process of completing the square
to solve a quadratic equation with a leading coefficient of 1. 
x2 + bx + c = 0
| 1. move the constant (number) term to the right side: |
move c |
| 2. take half of the coefficient of the x term: |
find 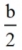 |
| 3.square this result: |
get 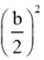 |
| 4. add this value to both sides of the equation: |
balance equation |
| 5. write the left side in factored form: |
write as 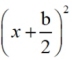 |
| 6. take the square root of both sides to find the solutions. |
solve |
|
Can you use completing the square on a quadratic equation
whose leading coefficient is not one?
Yes, simply divide through the equation by the existing leading coefficient,
to create a leading coefficient of one.
|

 Example of solving a quadratic equations by Completing the Square: Example of solving a quadratic equations by Completing the Square:
1. Check to see if the leading coefficient is one. If not, divide each term by the leading coefficient. |
x2 + 4x - 2 = 0
Leading coefficient is one. |
2. If there is a constant term on the left side of the equation, move the constant term to the right side. |
x2 + 4x = 2 |
3. Set up the problem to receive the addition of the value, c, which will create a perfect square trinomial on the left side. Inserting boxes may remind you to add the value to BOTH sides of the equation. |
|
4. To get the needed value (of c) for creating a perfect square trinomial, take half of the coefficient of the middle term (x-term) and square it. Add this value to both sides of the equation (put this value in the boxes). In this problem, half of 4 is 2, and 22 is 4.
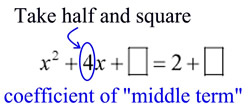
The term containing "x" is called the "linear term".
|
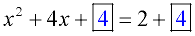 (Be sure to take note of the "sign" of half the coefficient of the middle term, as it will be used when factoring the perfect square trinomial.
(Be sure to take note of the "sign" of half the coefficient of the middle term, as it will be used when factoring the perfect square trinomial.
In this case, +2. )
|
5. Factor the perfect square trinomial on the left side. |
(x + 2)2 = 6 |
6. Now that there is a perfect square on the left side, take the square root of both sides. Solve for x. Be sure to remember to use "plus and minus" to arrive at the two roots of the equation.
Check your solutions in the original equation to see that they work.
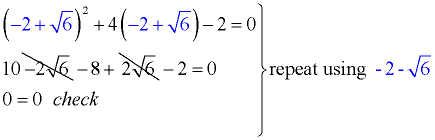
Always assume that answers are to be left in "exact" form (not rounded), unless told otherwise..
|
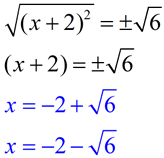
In real-world problems and for graphing, these values may be expressed as rounded decimal values:
x ≈ 0.4494897428
x ≈ -4.449489743
|

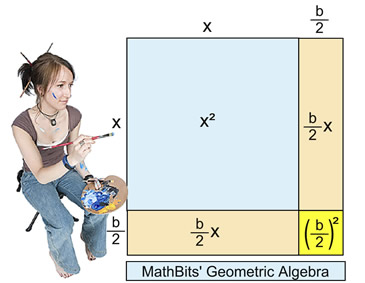
Let's verify, geometrically, that adding the square of half of the coefficient
of the x-term actually creates a perfect square trinomial.
 |
To solve x2 + bx + c = 0 by completing the square, we first move the constant, c, to the right side, x2 + bx = -c .
We then create a perfect square trinomial on the left by adding the square of half the coefficient of the x-term to both sides. That is, we add 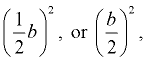 to both sides. Let's look at just the left side of that equation, and "paint a picture" of the perfect square trinomial. to both sides. Let's look at just the left side of that equation, and "paint a picture" of the perfect square trinomial.
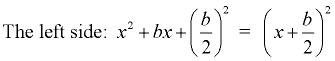 |

As seen in the picture, the area of the square can also be expressed as the sum of the areas of its parts:
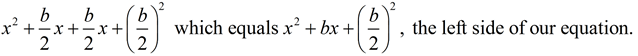 So both expressions are equivalent, verifying that this process creates a perfect square trinomial.
So both expressions are equivalent, verifying that this process creates a perfect square trinomial. |

 |
It will prove worthwhile to know this process as there will be other applications of completing the square. For example, completing the square will be used to derive important formulas, to create new forms of quadratics, and to discover information about conic sections (parabolas, circles, ellipses and hyperbolas).
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|