|
 |
Remember -- use your compass
and straightedge only! |
|
If you are asked to "construct" an angle of a specific size, it is expected that you will use your compass and straightedge. Do NOT use a protractor.
While the number of degrees in an angle can theoretically be any numerical value, certain limitations are placed upon formal constructions. Typically, angles such as 30º, 45º, 60º, 90º, 135º, 180º, 210º or 270º are examples of constructable angles. Additional angles can be constructed, such as angles of 15º and 22½º, by bisecting the constructable angles of 30º and 45º. There are, however, angles such as 51º and 73º, that cannot be constructed with only a compass and straightedge.
 |
The key to these angle constructions is remembering where you have seen these angles in previous constructions. |
|
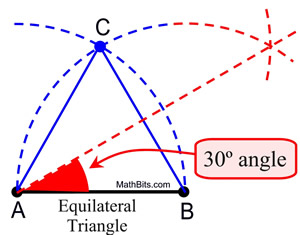
Angles of 60º, 30º or 15º |
All of these angles can be constructed, if you can construct the 60º angle. After constructing the 60º angle, simply bisect it to obtain the 30º angle, and bisect again to get the 15º angle.
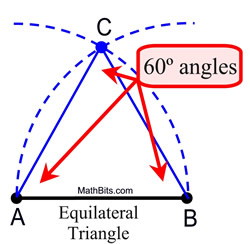
So, where have we already seen the construction of a 60º angle?
ANSWER: The angles in an equilateral triangle contain 60º. If you construct an equilateral triangle, you will have a 60º angle.
|
|
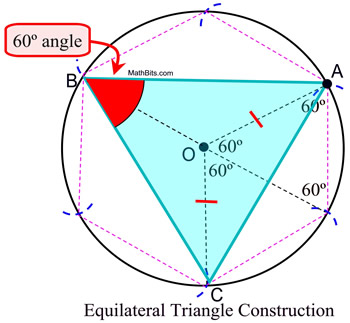
Note: The construction of the equilateral triangle inscribed in a circle (shown on the right above) starts with the construction of the regular hexagon. As shown in the diagram, the central angles in a regular hexagon also contain 60º.
|
This construction shows the 60º angle
of the equilateral triangle being bisected
to form two 30º angles.
Do you see the "bisect an angle"
construction, as it uses, and
extends,
some of the
existing arcs?
|
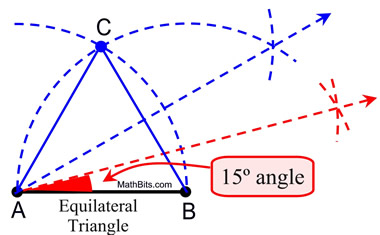
In this construction, we see the 30º angle
being bisected to form the 15º angles.
Again, this construction used an existing arc
and the extension of an existing arc, to
create the new bisector.
Do you see this new bisector? |
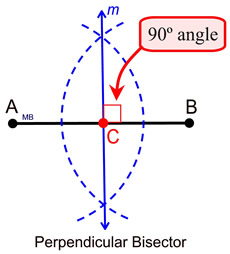
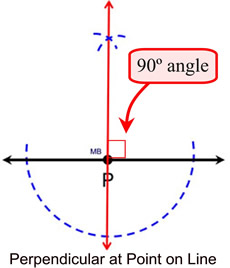
Both of these angles can be constructed, if you can construct a perpendicular (which creates a right angle containing 90º). Bisecting a 90º angle will create a 45º angle.
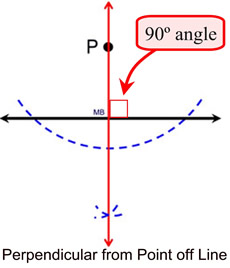
We have seen three constructions of perpendiculars: a perpendicular bisector, a perpendicular from a point on a line, and a perpendicular from a point off a line.
Note: The construction of a square will also create a 90º angle, but the constructions of the perpendiculars are easier and faster to create.
90º ANGLES:
|
|
|
45º ANGLES: (created from constructions shown above)
|
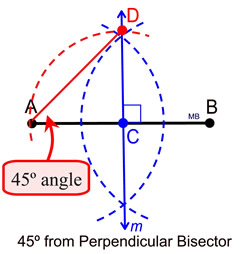
Instead of bisecting the 90º angle,
this construction shows the
simple
creation of a 45º-45º-90º triangle.
Place compass point at C, measure
span to A, swing arc from A to D,
making CA = CD .
Connect A to D to form ΔACD.
|
 All three perpendicular constructions shown above lend themselves
to being bisected to
form 45º angles.
All three perpendicular constructions shown above lend themselves
to being bisected to
form 45º angles. |
|
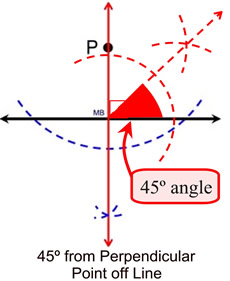
This construction shows bisecting
the 90º angle formed by the
perpendicular from a point off line
to form the 45º angle
. |
 See more about constructing angles at Construct: Rotations. See more about constructing angles at Construct: Rotations.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|