 |
Remember -- use your compass
and straightedge only! |
|
Perpendicular from a point ON a line. |
|
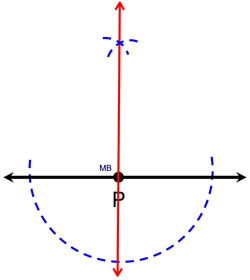
Given: point P on a given line
Construct: a line through P perpendicular to given line.
|
|
STEPS:
1. Place your compass point on P and swing an arc of any size below the line that crosses the line twice. You will be drawing at least a semicircle. (Note: While you can draw this arc above or below the line, below the arc keeps the construction lines from bumping into one another.)
2. Stretch the compass LARGER! (If you don't, your arcs will not cross, but will be tangnt at point P. Not helpful.)
3. Place the compass point where the arc crossed the line on one side and make a small arc above the line (the arc could be below the line if you prefer).
4. Without changing the span on the compass, place the compass point where the first arc crossed the line on the OTHER side and make another arc. Your two small arcs should be intersecting.
5. Using a straightedge, connect the intersection of the two small arcs to point P.
|
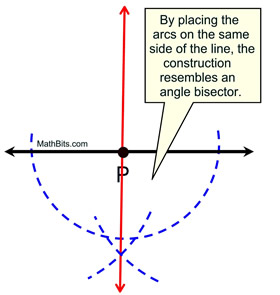
Does this construction
look familiar?
 |
|
Observe what is happening in the box above of the right. This construction is really just a special case of bisecting the angle. The angle, this time, just happens to be a straight angle (or stratight line) with 180º. When bisected, we have two 90º angles which establish the bisecting line as being perpendicular to the straight angle (or straight line). Remember, perpendicular lines form right angles.

Proof of Construction: This construction is actually another version of the construction of BISECT AN ANGLE. This construction bisected the straight angle P. Since a straight angle contains 180º, this construction created two 90º angles. Since two right angles have been formed, a perpendicular was created. If two straight lines intersect at right angles, the lines are perpendicular to each other.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|