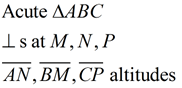We will continue our investigation of the
classical triangle centers with the
orthocenter.
|
A point of concurrency is the point where three or more lines intersect. |
|
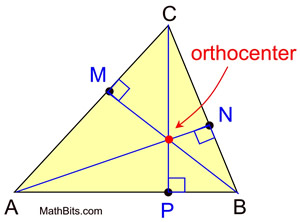
This discussion will focus on the name given to the point where the altitudes of a triangle
in that construction intersect. That point is called the orthocenter.
The term "ortho" is Greek implying right angles and perpendiculars.
Thus, the name "orthocenter" can be related to altitudes,
where we see right angles and perpendiculars.

 Orthocenter - concurrent altitudes
Orthocenter - concurrent altitudes
"ortho" - Greek meaning right angles, perpendicular
The three triangle altitudes are concurrent, meaning they
intersect on one common point.
That common point is called the orthocenter of the triangle.
Unlike the "incenter" and the "circumcenter", the orthocenter is not connected to a circle in relation to the triangle (such as is seen with the inscribed circle and the circumscribed circle).
An altitude of a triangle is a segment from any vertex perpendicular to the line containing the opposite side. We have seen that the construction of an altitude may fall outside the triangle.
We know that an altitude of a triangle is a segment. And we know that at least one altitude of a triangle (if not all) will reside inside the triangle. When looking for the point of concurency of the altitudes, it may be necessary to "extend" an altitude so it will meet up with the other altitudes to create the orthocenter.
The altitudes of a triangle are concurrent (they intersect in one common point).
The point of concurrency of the altitudes is called the orthocenter of the triangle.

The altitudes' point of concurrency (orthocenter) is not necessarily inside the triangle.
It may actually be inside the triangle, on the triangle, or outside of the triangle.
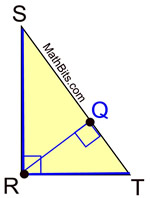
Let's take a look at the locations of the orthocenters in relation to
acute triangles, obtuse triangles and right triangles.
|
|
In a right triangle, the altitudes intersect at the right angle.
 |
 |
|

NOTE: The point of concurrency of the altitudes of a triangle will be the point where the perpendiculars, constructed from each vertex to the line containing the opposite side of the triangle, will meet. |
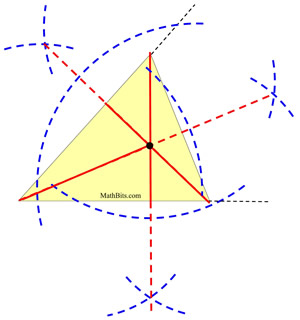
To construct the orthocenter:
We have seen how to construct an altitude of a triangle.
Simply construct the three altitudes of the triangle. The point where the altitudes intersect is the orthocenter.
Notice how it was necessary to extend the sides of the triangle for two of the constructions of a perpendicular from a vertex point to the opposite side.
The black point where the altitudes intersect is the orthocenter. |
 |
Actually, finding the intersection of only 2 altitudes will find the orthocenter.
Finding the third altitude, however, will ensure more accuracy of the find. |