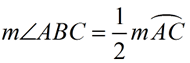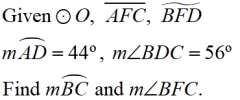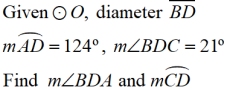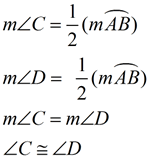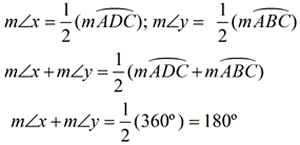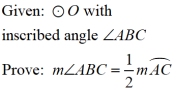|
Starting with this lesson, we will be investigating angles, associated with circles,
whose measurement formulas are theorems.
|
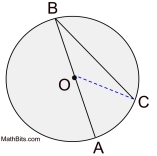
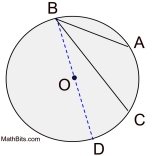
A inscribed angle of a circle is an angle whose vertex is a point on the circle and whose rays contain two other points on the circle (that is, the rays are chords). |
|
Inscribed Angle (theorem)
The measure of an inscribed angle equals
½ the measure of its intercepted arc.
Inscribed Angle = 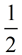 Intercepted Arc Intercepted Arc
 |
In the diagram at the right, ∠ABC is an inscribed angle with an intercepted minor arc from A to C.
|
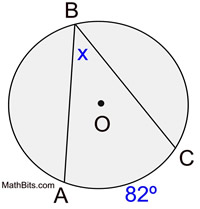 m∠ABC = 41º
m∠ABC = 41º |
|

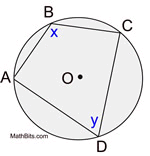
Example 1:
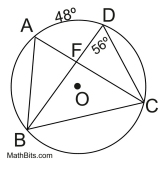
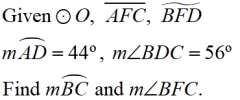
How many inscribed angles can
be seen in this diagram?
|
Solution:
• If the arc is 48º, then the inscribed angle, m∠ABD = 24º.
• If m∠BDC = 56º, then the minor arc from B to C has a measure of 112º. Since ∠BAC also intercepts this arc, m∠BAC = 56º.
• In ΔBAF we have angles of 56º and 24º, making m∠AFB = 100º
• Since ∠BFC is supplementary to∠AFB,
m∠BFC = 80º.
There are 8 inscribed angles.
|
|
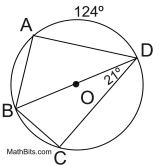
Example 2:
|
Solution:
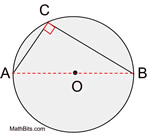
• With the given diameter, there are two semicircles. ∠A and ∠C are right angles.
• m∠BDC = ½ m of the minor arc from B to C.
(21 is half of 42)
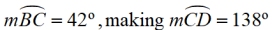
since 42 + 138 = 180 for the semicircle arc
• 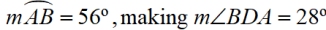 For the arc: 180 - 124 = 56
For the arc: 180 - 124 = 56
For the angle: ½ of 56 = 28
|
|

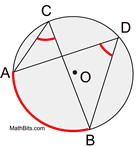
Theorems Associated with Inscribed Angles:
 
In a circle, inscribed angles that intercept the same arc are congruent. |
 |
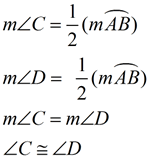 |
|
Additional Theorems related to cyclic quadrilaterals:
• A cyclic parallelogram is a rectangle.
• If a pair of opposite sides of a cyclic quadrilateral are equal in length,
then the diagonals are also equal in length.
• The measure of the exterior angle of a cyclic quadrilateral is equal
to the measure of the interior opposite angle.
• In a cyclic quadrilateral, the product of the diagonals equals
the sum of the products of its two pairs of opposite sides.

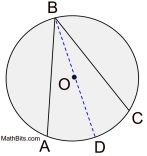
PROOF of the theorem on measuring an inscribed angle:
There are actually three cases for the proof of this theorem.
CASE 1: the center of the circle lies on one of the inscribed angle's rays (one ray is a diameter)
CASE 2: the center of the circle lies in the interior of the inscribed angle
CASE 3: the center of the circle does not lie in the interior of the inscribed angle

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|