1. 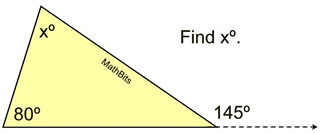 |
Solution:
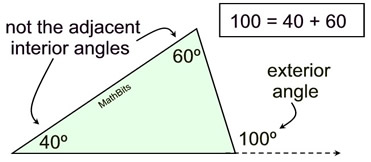
Using the Exterior Angle Theorem
145 = 80 + x
x = 65
Now, if you forget the Exterior Angle Theorem, you can still get the answer by noticing that a straight angle has been formed at the vertex of the 145º angle. See Example 2. |
2. 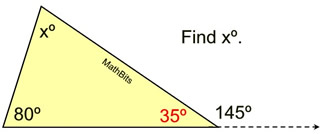 |
Solution: I forgot the Exterior Angle Theorem.
The angle adjacent to 145º will form a straight angle along with 145º adding to 180º. That angle is 35º.
Now use rule that sum of ∠s in Δ = 180º.
35 + 80 + x = 180
115 + x = 180
x = 65 |