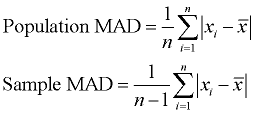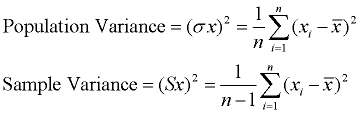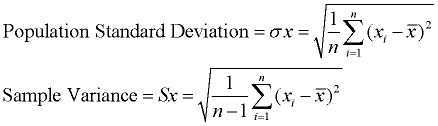|
 Note: NY NGMS will focus on the "Sample Standard Deviation".
When dealing with statistical data, it is important to distinguish between
" population" data sets and " sample" data sets.
 |
A population data set contains all members of a specified group (the entire list of possible data values).
Example: A population may be "ALL people living in the US." (huge number)
[Utilizes the count n in formulas.] |
|
|
A sample data set contains a part, or a subset, of a population. The size of a sample is always less than the size of the population from which it is taken.
Example: A sample may be "ALL people living in one US city." (smaller number)
[Utilizes the count n - 1 in formulas.] |
|
When calculating the formulas for mean absolute deviation (MAD), variance, and standard deviation, it is important to know if you are working with an entire population (where you have all of the possible data), or if you are working with only a sample (a part) of the data. In addition, if you are using a sample of the data, you need to know if you will be making generalizations about the entire population, based upon this sample.
The only difference between the formulas in each section is division by n or n - 1.
Read more about these formulas under Measures of Spread.
Note: When working with "sample data sets", statisticians use the notation n for the 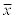number of data entries and  for the mean, however, when working with "population data sets", they use N for the number of data entries and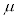 
for the mean. In Algebra 1, to avoid confusion and to coordinate with the notations used by the TI-84+ calculators, we will be using n for the number of data entries and 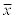for the mean for both population and sample data sets (as seen above).
Let's take a look at an example dealing with "population" versus "sample".
(a)
A statistical study of the heights of all fourteen year old boys in your Algebra class. |
This task is only dealing with the heights of fourteen year old boys in one specific class. The intent is not to estimate the heights of all fourteen year old boys in your school or in the world. Normally, this situation would be an example of a "sample" population, but since you have the "entire" population of boys in your Algebra class available, you will be dealing with the that smaller population (dividing by n).
(b)
A statistical study of the heights of all fourteen year old boys in the world. |
In this situation, the population is extremely large. There is actually no way of obtaining all of the data in the population. You simply will not have all of the data available for your use. You will need to use a sample of the population. It will be necessary to "estimate" the population's heights based upon the heights of the sample population. You will be dealing with the sample (dividing by n - 1). |
Most "real world" studies deal with sample data sets.
In these cases, it is unrealistic (or impossible) to gather ALL of the population's data.
Instead, generalizations will be made about the entire population based upon the
statistics found in a sample of the population.
... the weight of adult German Shepherd dogs.
... the
number of bicycles.
... the number of cell phones.
... the
ages of college seniors.
... the number of people who viewed an eclipse.
... the height of mature oak trees.
|
It would be impossible to have access to "every" piece of data in existence in these situations. |
 Population or Sample? Give it a try: |
Directions: For the following problems, decide if the situation is dealing with a "population" data set, or with a "sample" data set. Explain your decision.
1. Mrs. Smith wants to do a statistical analysis on students' final examination scores in her math class for the past year. Should she consider her data to be a population data set or a sample data set?
2. A group of students surveys 100 students from their freshman class to determine the number of pets in each student's household. The group plans to compute statistical findings on their data and generalize these findings to the homes of all freshmen students. Should the group consider their data to be a population data set or a sample data set?
Summary: |
Use "population" when:
1. you know you have the entire population.
2. you have a sample of a larger population, but you are only interested in this sample (and you will not be generalizing your findings to the entire larger population). |
|
For calculator info on
population
versus sample
click here.
|
|
|
Use "sample" when:
1. you have a sample of a larger population, and you wish to generalize your findings from this sample to the entire larger population from which this sample was taken. The sample will be used as an estimate of the population. |
|
Some questions will clearly state whether you are working with a population or a sample. If no statement is present, ask yourself if the statistical findings will be used to describe a larger group. If the answer is yes, you are working with a sample.
Real world statisticians primarily work with sample situations, since real-world data can be overwhelmingly large.
|
|
Note: The practice of dividing by n - 1 (instead of n) when working with a sample of the entire population, produces a slight difference in the final calculation. This slight difference allows the sample to give a better mathematical estimate of the population. Think of dividing by n - 1 (instead of n) in the sample as a means of "compensating" for the fact that we are working with a sample of the population, rather than with the entire population. It statistically gives the best estimate.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
