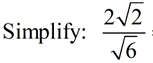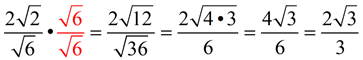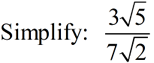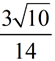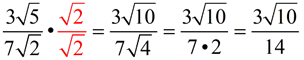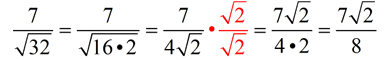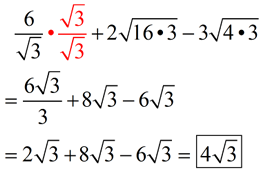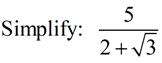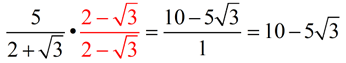|
(For this lesson, the term "radical" will refer to "square root".)
Like multiplication of radicals, you can divide radicals
with different radicands (the number under the radical symbol),
Dividing radicals makes use of the "Quotient Rule" stated below.
Quotient Rule
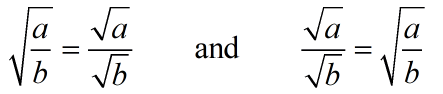
where a ≥ 0, b > 0
"The square root of a quotient is equal to
the quotient of the square roots of the numerator and denominator." |
|
"The square roots of a numerator and a denominator is equal to the square root
of the quotient." |
|
|
Dividing Radicals: When dividing radicals (with the same index), divide under the radical, and then divide any values in front of the radical(that is, any values that are multiplied times the radicals). |
|
If the radicals are being multiplied by a number in front of the radical:
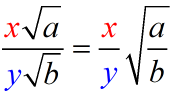
Divide the coefficients (x / y) and divide the radicands (a / b).
(This only applies to radicals with the same index.)
 |
Divide coefficients outside the radicals.
Divide numbers inside the radicals.
(assuming radicals have the same index)
|
|

|
|
|
ANSWER: 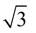 |
| |
Divide under the radicals. 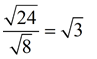
|
|
|
ANSWER: 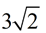 |
| |
Divide the coefficients in front of the radicals.
And divide the numbers under the radicals.
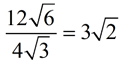
|
|
|
ANSWER: 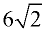 |
| |
Divide out front and divide under the radicals. 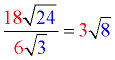
Then simplify the result. 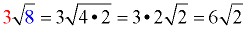
|
|
|
ANSWER: 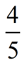 |
| |
Let's look at this solution in two methods:
Method 1: Divide
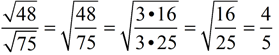
The numbers under the radicals were
divided to form a fraction under the
radical. The fraction was reduced.
Two perfect squares were found.
|
Method 2: Simplify first:
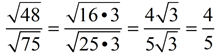
Simplifying FRST will save time. If there had not been two perfect squares, the first method would have required further work.
|
 Remember that both methods worked. But, if you simplify first, you will not be faced with additional (or more difficult) simplifications when you don't end up with perfect squares under the radical. Remember that both methods worked. But, if you simplify first, you will not be faced with additional (or more difficult) simplifications when you don't end up with perfect squares under the radical.
|
|
|

Rationalizing the Denominator:
When simplifying radicals, it is considered bad form to leave a radical in the denominator of a fraction. Let's take a look at how to remove a radical from the denominator based upon the type of term in the denominator. |
Why do we need to do this? What's wrong with leaving a radical in the denominator?
These are both good questions. The most prominent answer is that rationalizing the denominator is a historical precedent. Before computers and calculators (when mathematics was done "by hand"), there were valid reasons for getting a radical out of a denominator. By creating a rational, whole number denominator, computations such as addition, subtraction, long division, and even comparing similar terms, could occur more easily. It was also felt that a rational denominator allowed for a better comprehension of what the quantity represented. Rationalizing the denominator became a convention that added consistency to working with radicals.
So, there is nothing "wrong" with using a radical denominator, especially in today's technological world. Rationalizing the denominator does, however, allow for an alternative view of the fraction that will be beneficial for combining like terms when working with other radical values. It will also give a better initial grasp of the value of the fraction.
HINT: If asked to "rationalize the denominator" on a test or quiz, do NOT give the
answer that there is "nothing wrong with using a radical denominator".

|
|
ANSWER: 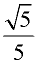 |
| |
This fraction will be in simplified form when the radical is removed from the denominator.
You need to turn this
"irrational" radical denominator into a "rational" number.
We know that squaring and square rooting are inverse operations. So, squaring the fraction would remove the radical denominator, BUT it would also change the value of the fraction. NOT A GOOD IDEA!!!
We will use this idea of squaring, but in a sneaky manner. We know that "1" is the multiplicative identity - you multiply any number by "1" and the number will not be changed. So, we are going to create a fraction that when multiplied by our problem will create a perfect square in the radical denominator, but will not change the value of the original fraction.
 THE FRACTION WE CREATE WILL EQUAL ONE! THE FRACTION WE CREATE WILL EQUAL ONE!
Multiply the top and bottom of the given fraction by the square root radical that appears in the denominator (in this case multiply by 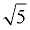 ). We will be multiplying by "1". We will create a perfect square in the radical denominator and we will not change the original fraction's value. ). We will be multiplying by "1". We will create a perfect square in the radical denominator and we will not change the original fraction's value.
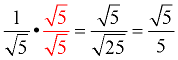 You have just "rationalized" the denominator! You have just "rationalized" the denominator!
|
 |
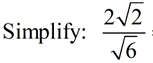 |
ANSWER: 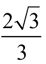 |
| |
After multiplying by "one", the numerator needs further simplifying.
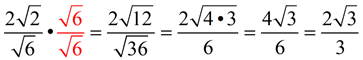
|
 |
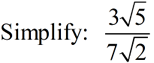 |
ANSWER: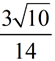 |
| |
While we need to remove the radical 2 from the denominator, we do not need to remove the "7". Just carry the 7 along and concentrate on eliminating the radical 2.
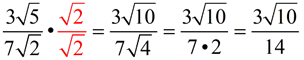
|
 |
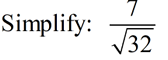 |
ANSWER: 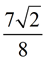 |
| |
The radical in this problem is a larger radical, but it can be reduced.
If we reduce FIRST, we will be able to work with a smaller radical value.
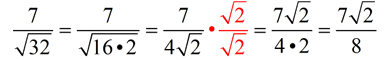
|
 |
 |
ANSWER: 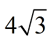 |
| |
 This is where getting a rational denominator is helpful. This is where getting a rational denominator is helpful.
These three terms can be combined into one term.
We can create one term that is the exact answer, and not an estimate.
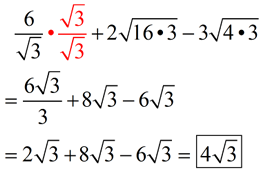
|
 Extra
Extra |
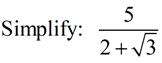 |
ANSWER: 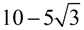 |
| |
That "plus" sign in the denominator creates a problem.
We need a different approach when the denominator is a "binomial" containing a radical.
Remember: under the Multiplying Radicals lesson, we saw a special case where multiplying two "conjugates" creates a rational number. This is the approach we will be taking with this problem.
The conjugate for this problem will be the same denominator with the "+" sign changed to a "-" sign.
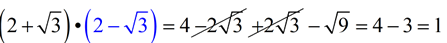
Of course, we will continue to multiply by "one" so as not to change the fraction.
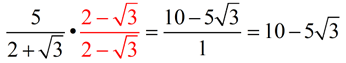
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
Topical Outline | Algebra 1 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use Contact Person: Donna Roberts
|
|

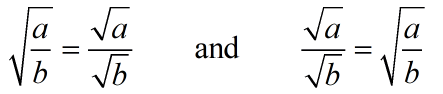
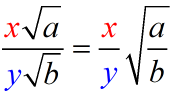

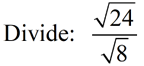
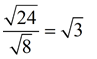
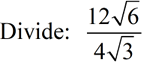
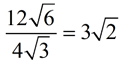
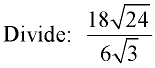
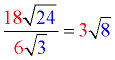
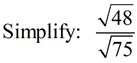
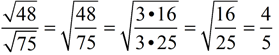
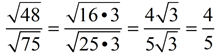
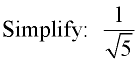
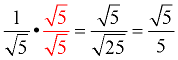 You have just "
You have just "