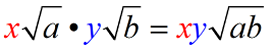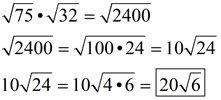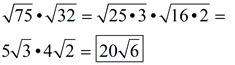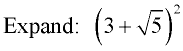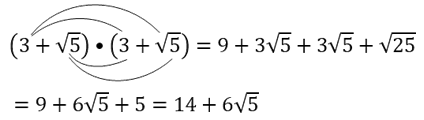|
(For this lesson, the term "radical" will refer to "square root".)
Unlike adding and subtracting radicals, you can multiply radicals
with different radicands (the number under the radical symbol),
Multiplying radicals makes use of the "Product Rule" stated below.
Product Rule
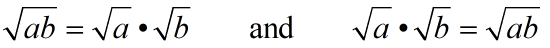where a ≥ 0, b≥ 0
"The square root of a product is equal to
the product of the square roots of each factor." |
|
"The product of the square roots of two terms is equal to the square root of the product
of the two terms." |
|
|
Multiplying Radicals: When multiplying radicals (with the same index), multiply under the radical, and then multiply any values in front of the radical (that is, any values that are multiplied times the radicals). |
|
If the radicals are being multiplied by a number in front of the radical:
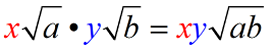
Multiply the coefficients (x • y) and multiply the radicands (a • b).
(This only applies to radicals with the same index.)
 |
Multiply coefficients outside the radicals.
Multiply numbers inside the radicals.
(assuming radicals have the same index)
|
|
|
|
ANSWER:  |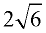
| |
Multiply the values under the radicals.
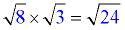
Then simplify the result.
 |
 |
 |
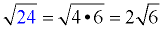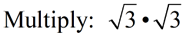ANSWER: 3 |
| |
Multiply under the radicals.
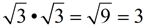
When you multiply a square root times itself, you create a perfect square under the square root symbol (as the radicand). We know that squaring and that square rooting are inverse operations (undoing one another). The result is the radicand.
|
|
|
ANSWER: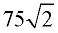 
|
| |
Multiply out front and multiply under the radicals.
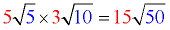
Then simplify the result. Radical 50 can be simplified.
|
|
|
|
|
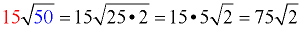
ANSWER: 16 |
| |
Multiply under the radicals.
Remember that the number in front of radical 2 is implied to be " 1".
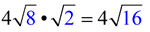
Then simplify the result.
|
|
|
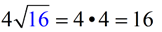
ANSWER:  |
| |
These are two rather large radicals to multiply, and each of these radicals can be initially simplified (reduced). Let's look at two solutions.
First Method:
Let's multiply first, then simplify.
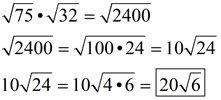
A very large number was created
in this number that then needed
to be simplified.
|
Second Method:
Let's simplify first, then multiply.
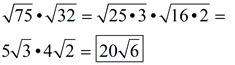
Simplifying first avoided all of that
work with the large number
simplification.
|
 Remember that both methods worked. But, if you simplify first, you will not be faced with attempting to simplify very large number values for your final answer, thus reducing simplifying errors.
|
 |
 |
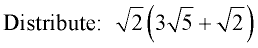ANSWER:  |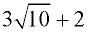
| |
Distribute across the parentheses.
Remember there is an implied "1" in front of  .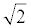
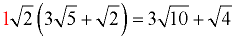
Then simplify the result.
|
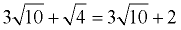
Extra |
|
ANSWER:  |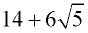
| |
This problem is a binomial (the sum of 2 separate terms) being squared (multiplied times itself).
We will need to apply the distributive property for multiplying binomials.
The pattern for multiplying two binomial terms is shown below.
Then combine like terms.
Basically: each term in the first binomial gets multiplied times each term in the second binomial. Add all results together.
You may see the steps in this process referred to as FOIL (first, outer, inner last).
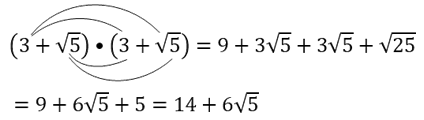
Note: If a negative sign (or subtraction) is involved:
•
the subtraction symbol translates to adding a negative value.
•
the negative sign "travels" with the number to which it is assigned.
|
Extra
|
|
ANSWER:  |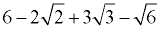
| |
Use the distributive property for multiplying binomials shown in Example 6.
In this problem, the subtraction sign will be interpreted as "adding a negative square root of two."
There are NO like terms to be combined, so the entire list of terms is the answer.
|
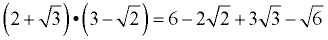
Extra |
 |
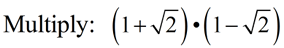ANSWER: -1 |
| |
Something interesting is happening in this solution,
Notice the middle terms dropping out.
The final answer becomes the product of the first terms in each binomial, added to the product of the second terms in each binomial. The "middle terms" drop out. This usually does NOT happen when multiplying binomial expressions, as seen in the previous examples.
The reason this is happening in this case, is that the binomial terms are exactly the SAME, except for the arithmetic operators between the terms in each binomial. These arithmetic operators (addition and subtraction) are opposites. This creates middle terms in the multiplication that drop out. In later courses, you will see that such binomial terms are referred to as "conjugates".
Note: Multiplying two conjugates creates a rational number. |
|
|
