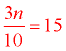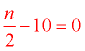|
We are familiar with translating words into mathematical operations in the writing of algebraic expressions. The chart below is a reminder of how certain words are connected to mathematical operations. This same chart will be helpful as we examine linear equations.
A sampling of words used to represent mathematical operations:
ADD |
SUBTRACT |
MULTIPLY |
DIVIDE |
add
sum
increased by
more than
exceeds
total
plus
in all
gain
deposit |
subtract
difference
decreased by
fewer
less than *
diminished by
minus
take away
withdraw
reduced by
|
multiplied by
product
of
times
double
triple
twice
|
divide
quotient
per
divided equally
split into
fraction
ratio of
|
* be careful using "less than" - it reverses the order of things.
It is not written in the order it is read.
"5 less than 8" is written 8 - 5 and not 5 - 8
"3 less than n" is written n - 3 and not 3 - n

We are now ready to extend this skill of translating words into algebraic expression
to include algebraic equations.
 Algebraic Equations: Algebraic Equations:
Unlike expressions, algebraic equations contain an equal sign.
EQUAtion  EQUAl sign EQUAl sign
You will still encounter the "words" used to represent mathematical operations,
as shown in the chart at the top of the page. To that list, we can now add a sampling of words that imply "an equal sign".
EQUAL |
is,
are, was, were, equivalent to, same as, yields, gives |
Remember to continue to look for commas, to help you group your terms.

|
When trying to create equations, you may find it difficult to quickly arrive at an answer. When this happens, it is often helpful to make up a numerical example from the situation so you can see how the numbers are related to one another. In addition, a numerical example is useful for checking to see if the equation you wrote is accurate.
|
 |
|
| |
Verbal Statement |
Algebraic Equation |
1. |
Three times a number, divided by ten equals fifteen. |
|
2. |
Ten less than the quotient of a number and two is zero. |
|
3. |
Twelve more than the product of a number and two is thirty-six. |
2n + 12 = 36 |
4. |
Represent the cost of access to a movie web site which charges a $5 fee for the first month, and then $28 a month for continued access after the first month.
Numerical Example: For 4 months the cost would be: Cost = $5 + $28•(4-1). Replace 4 with m for number of months. |
c = cost, m = months
c =
5 + 28(m - 1) |
5. |
If chocolate doughnuts cost $1.10 and chocolate chip muffins cost $2.25, how many of each can you purchase for $20?
Numerical Example: The cost of 3 doughnuts and 2 muffins will be: Cost = $1.50•3 + $2.25• 2. Replace 3 with d for doughnuts, 2 with m for muffins, and Cost with $20.
|
d =doughnuts, m = muffins
20 =
1.50d + 2.25m |
6. |
Express the area of a rectangle whose length is twice its width decreased by 6.
Numerical Example: If the width is 10, the length is 14, then the area, A = 10 • 14. Just replace 10 with w for width, and 14 with 2w - 6 for the length. |
A = area, w = width
A = w • (2w - 6) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|