Mathematics is often referred to as being another language. With this idea in mind, let's take a look at how to translate words from English into mathematics, in this case algebra.

bullet Algebraic Translations:

When translating mathematical expressions written in word form (verbal expressions), you need to know how to represent the unknown quantities and the operations assigned to the expressions. This skill of translating expressions is dependent upon the language that is being used in the description of the expression.

For example, consider the expression which is read "exceeds n by four".
The unknown quantity in this expression is given to be "n". But, what "mathematical operation" is represented by the word exceeds?
If you guessed that "exceeds" implies addition, you are correct.
This expression is mathematically written as n + 4.

Below are some of the most common words and phrases used in translating expressions,
together with the operations they represent.
This is not an exhaustive list. You may also find other words that apply.

A sampling of words used to represent mathematical operations:

ADD
SUBTRACT
MULTIPLY
DIVIDE
add
sum
increased by
more than
exceeds
total
plus
in all
gain
deposit
subtract
difference
decreased by
fewer
less than *
diminished by
minus
take away
withdraw
reduced by
multiplied by
product
of
times
double
triple
twice
divide
quotient
per
divided equally
split into
fraction
ratio of

* be careful using "less than" - it reverses the order of things.
It is not written in the order it is read.
"5 less than 8" is written 8 - 5 and not 5 - 8
"3 less than n" is written n - 3 and not 3 - n

dividerdash

smallstar Also, be careful of the placement of commas in statements.
Consider: Is there a difference between these two statements?

• the sum of a and b, divided by 3

• the sum of a and b divided by 3

The answer is "yes". (No comma in the second statement.)
But there is also a mathematical difference between these statements.

In the first statement, "the sum of a and b, divided by 3",
the comma indicates the completion of the concept presented before the comma.
The a and b will be added BEFORE considering the division by 3.
Think of the statement as "find the sum of a and b", pause (the comma), then "divide by 3".
Mathematically it looks like: 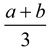ab3a

In the second statement, "the sum of a and b divided by 3",
there is no comma after the b, so there is no "pause" in the statement.
The statement is interpreted as the adding of (a) and (b divided by 3).
You are simply "adding" what comes before the word "and" to what comes after the word "and".
Mathematically it looks like: 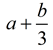ab3b.

dividerdash

expinS

 
In these examples, we will be using "n" to represent "a number".
Actually, any letter can be used, such as x, a, b, etc.
 
Verbal Statement
Algebraic Expression
1.
 Five increased by four times a number.
5 + 4n
2.
Eight less than twice a number.
2n - 8
3.
Three times a number, increased by 9.
3n + 9
4.
The product of 4, and a number decreased by 7
4 (n - 7)
5.
The number of feet in x yards.
3x
6.
Express the width of a rectangle which is seven less than its length, l.
l - 7
7.
A number repeated as a factor 3 times.
n • n • n = n3
8.
The quotient of fourteen and triple a number.
14 / (3n)
9.
Twelve times, a number increased by 6.
12 (n + 6)

 


In a problem like Example #8, remember that 14/3n is not the same as 14/(3n).
hint gal

frac1

frac2

dividerdash

It may be necessary to reverse this situation.
Given the algebraic expression, create a possible verbal statement.

10.
Given 3n - 2, write a verbal expression that matches this mathematical expression.
Here are five possible answers:
• three times a number decreased by two
• triple a number minus two
• two less than three times a number
• three times a number diminished by two
• the product of three and a number, reduced by two

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".
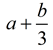