Find three consecutive even integers whose sum is 18.
"Consecutive" means "one after the other". Consecutive integers (such as 1, 2, 3) are represented as x, x+1, x+2.
Consecutive even integers (such as 2, 4, 6) are represented as x, x+2, x+4.
Consecutive odd integers (such as 3, 5, 7) are represented as x, x+2, x+4.
Check: 4 + (4 + 2) + (4 + 4) = 18
4 + 6 + 8 = 18
18 = 18
|
Let n = the first even number
n + 2 = the second even number
n + 4 = the third even number
Create the equation:
n + (n + 2) + (n + 4) = 18
Solve the equation:
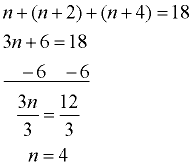
The numbers are 4, 6, and 8. |